क्या आप चतुर्भुज की जानकारी पढ़ना चाहते हैं तो आप सही पेज पर आए हैं इस आर्टिकल में आप चतुर्भुज की समस्त जानकारी पढ़ सकते हैं।
पिछले पेज पर हमने त्रिभुज की जानकारी शेयर की हैं यदि आपने अभी तक उस आर्टिकल को नहीं पढ़ा तो लिंक पर क्लिक करके पढ़ सकते हो।
चलिए आज हम चतुर्भुज की जानकारी को पढ़ते और समझते हैं।
Table of Contents
चतुर्भुज किसे कहते हैं
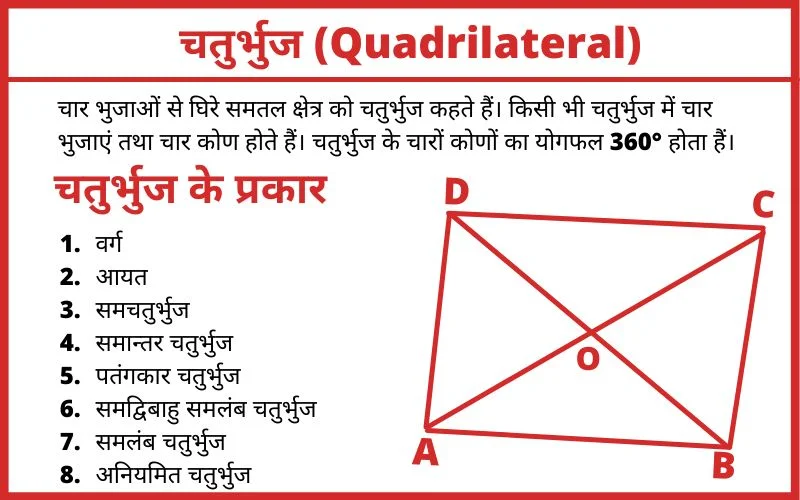
चार भुजाओं से घिरे समतल क्षेत्र को चतुर्भुज कहते हैं। चतुर्भुज में चार भुजाएं तथा चार कोण होते हैं।
चतुर्भुज के चारों कोणों का योगफल 360° होता हैं।
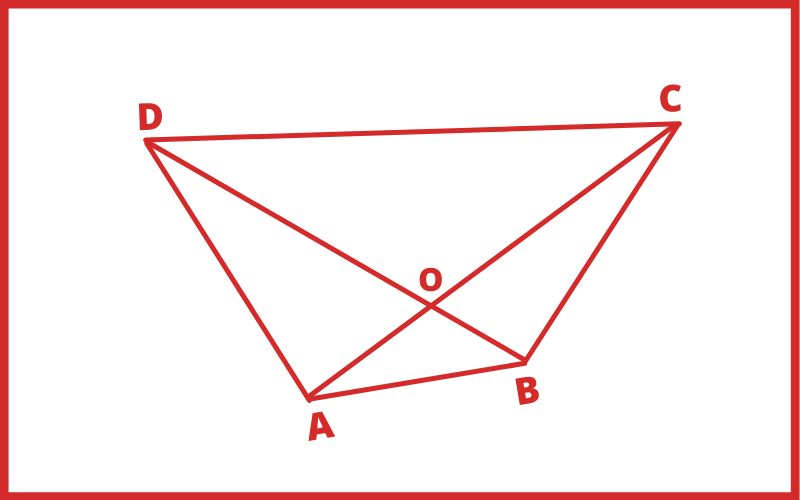
दिए हुए चतुर्भुज में दो विकर्ण खीचें गए हैं पहले विकर्ण को AC तथा दूसरे विकर्ण को BD नाम से प्रदर्शित करते हैं।
चतुर्भुज की ऐसी दो भुजाएँ जिसका कोई उभयनिष्ठ बिंदु न हो सम्मुख भुजाएँ कहलाती हैं।
AB, CD के सम्मुख भुजाएँ हैं एवं AD, BC के सम्मुख भुजाएँ हैं।
∠A + ∠B + ∠C + ∠D = 360°
चतुर्भुज के सूत्र
- चतुर्भुज का क्षेत्रफल = ½ × विकर्णों का गुणनफल
- चतुर्भुज के क्षेत्रफल = ½ × d(h₁ + h₂)
चतुर्भुज के प्रकार
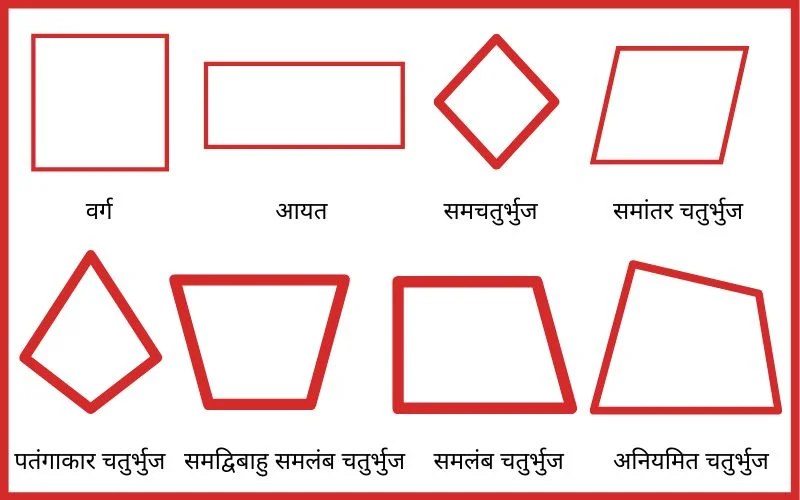
चलिए नीचे चतुर्भुज के प्रकारों को विस्तार से पढ़ते और समझते हैं।
1. वर्ग
चार भुजाओं से घिरी वह आकृति जिसकी चारो भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण अर्थात 90° का हो, उसे वर्ग कहते हैं।
वर्ग के सूत्र
- वर्ग का क्षेत्रफल = (एक भुजा)² = a²
- वर्ग का क्षेत्रफल = ½ × (विकर्णो का गुणनफल) = ½ × AC × BD
- वर्ग की परिमिति = 4 × a
- वर्ग का विकर्ण = एक भुजा × √2 = a × √2
- वर्ग का विकर्ण = √2 × वर्ग का क्षेत्रफल
2. आयत
चार भुजाओं से घिरी वह आकृति, जिसमें आमने सामने की भुजाएँ समान्तर और बराबर होती हैं तथा प्रत्येक कोण समकोण होता हैं आयत कहलाता हैं।
आयत के सूत्र
- आयत का परिमाप = 2(लम्बाई + चौड़ाई)
- आयत का क्षेत्रफल = लंबाई × चौड़ाई
- आयत का विकर्ण =√(लंबाई² + चौड़ाई²)
3. समचतुर्भुज
एक ऐसा चतुर्भुज जिसकी चारों भुजाएँ समान हों समचतुर्भुज कहलाता हैं।
समचतुर्भुज के सूत्र
- समचतुर्भुज का क्षेत्रफल = ½ (विकर्णों का गुणनफल)
- समचतुर्भुज का परिमाप = 4 x भुजा
4. समान्तर चतुर्भुज
जिस चतुर्भुज के आमने-सामने की भुजाएँ समान एवं समानान्तर हो समान्तर चतुर्भुज कहलाता हैं।
समान्तर चतुर्भुज के सूत्र
- समान्तर चतुर्भुज का क्षेत्रफल = लम्बाई x चौड़ाई
- समान्तर चतुर्भुज का परिमाप = 2 (लम्बाई + चौड़ाई)
5. विषमकोण समचतुर्भुज
चार भुजाओं से घिरी वह आकृति, जिसमें चारों भुजाएं बराबर हों, लेकिन एक भी कोण समकोण न हो, उसे विषमकोण समचतुर्भुज कहते हैं।
विषमकोण समचतुर्भुज के सूत्र
- विषमकोण चतुर्भुज का क्षेत्रफल = ½ × दोनों विकर्णो का गुणनफल
- विषम कोण समचतुर्भुज की परिमाप = 4 × एक भुजा
- समचतुर्भुज में, (AC)² + (BD)² = 4a²
6. समलम्ब चतुर्भुज
एक ऐसा चतुर्भुज जिसकी भुजाओ का एक युग्म समान्तर हो समलम्ब चतुर्भुज कहलाता हैं।
समलम्ब चतुर्भुज के सूत्र
- समलम्ब चतुर्भुज का क्षेत्रफल = ½ × ऊँचाई × समान्तर भुजाओं का योग
- समलम्ब चतुर्भुज का क्षेत्रफल = ½ × h × (AD + BC)
7. चक्रीय चतुर्भुज
ऐसा चतुर्भुज जिसके चारों शीर्ष एक वृत्त पर स्थिर हो चक्रीय चतुर्भुज कहलाता हैं।
जैसे :- ∠A + ∠C = 180°, ∠B + ∠D = 180°
8. पतंगाकार चतुर्भुज
पतंगाकार में आसन्न भुजाओं के दो युग्म बराबर लम्बाई के होते हैं। अर्थात एक विकर्ण, चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता हैं।
इसलिए समान भुजाओं के दो युग्मों के बीच के कोण बराबर होते हैं। और दोनों विकर्ण एक दूसरे के लम्बवत होते हैं।
चतुर्भुज की विशेषताएं
- चतुर्भुज के चारों कोणों का योग 360° होता हैं।
- इसका मान चार समकोण के बराबर या 2π रेडियन होता हैं।
- आयत के विकर्ण समान होते है, लेकिन एक दूसरे पर लम्बवत नहीं होते हैं।
- विषमकोण समचतुर्भुज के विकर्ण समान नही होते लेकिन एक दूसरे पर लम्बवत होते हैं।
- पंचभुज के कुल अंतः कोण का योग 540° अर्थात 6 समकोण होता हैं।
- पंचभुज में विकर्ण की संख्या 5 होती हैं।
- षष्टभुज के कुल अंतः कोण का योग 720° अर्थात 8 समकोण होता हैं।
- अष्टभुज के कुल अंतः कोण का योग 1080° यानि 12 समकोण होता हैं।
चतुर्भुज के सवाल
Q.1 एक वर्ग की परिमाप 24 मीटर हैं और दूसरे वर्ग की परिमाप 32 मीटर हैं। एक वर्ग जिसका क्षेत्रफल दोनों वर्गों के क्षेत्रफल के बराबर हो परिमाप होगा?
A. 40 मीटर
B. 20 मीटर
C. 30 मीटर
D. 50 मीटर
हल:- प्रश्नानुसार,
24 मीटर परिमाप वाले वर्ग की भुजा = 24/4
= 6 मीटर
32 मीटर परिमाप वाले वर्ग की भुजा = 32/4
= 8 मीटर
दोनों वर्गों का क्षेत्रफल = 6²+ 8²
= 36 + 64
= 100 वर्ग मीटर
तीसरे वर्ग का क्षेत्रफल = 100 मीटर
भुजा = 10 मीटर
परिमाप = 4 × 10
= 40 मीटर
Ans. 40 मीटर
Q.2 एक वर्ग तथा आयत दोनों के परिमाप 48 मीटर हैं। दोनों के क्षेत्रफल में 4 वर्ग मीटर का अंतर हैं। आयत की माप (मीटर में) हैं?
A. 20, 4
B. 18, 6
C. 14, 10
D. 22, 17
हल:- माना आयत की लम्बाई x मीटर हैं।
आयत की चौड़ाई = (24 – x) मीटर
तथा वर्ग की एक भुजा = 48/4
= 12 मीटर
प्रश्नानुसार,
(12)² – x (24 – x) = 4
144 – 24x + x² = 4
x² – 24x + 140 = 0
x = 14, 10
अतः आयत की माप 14 मीटर और 10 मीटर हैं।
Q.3 एक आयताकार मैदान की लंबाई और चौड़ाई का अनुपात 5 : 3 हैं यदि मैदान का क्षेत्रफल 960 मीटर² हो तो मैदान के चारों और तीन बार लपेटने में कुल कितना तार लपेटना पड़ेगा?
A. 150 मीटर
B. 240 मीटर
C. 241 मीटर
D. 284 मीटर
हल:- आयताकार मैदान की लंबाई = 5x मीटर
तथा आयताकार मैदान की चौड़ाई = 3x मीटर
आयताकार मैदान का क्षेत्रफल = लम्बाई × चौड़ाई
630 = (5x) × (3x)
630 = 15 x²
x² = 630/15
x² = 64
x = 8 मीटर
अतः लम्बाई = 5x
5 × 8 = 40 मीटर
तथा चौड़ाई = 3x
3 × 8 = 24 मीटर
आयताकार मैदान का परिमाप = 2 (लम्बाई + चौड़ाई)
= 2(40 + 24)
= 2 × 64
= 128 मीटर
अतः तीन चक्कर में लपेटा गया कुल तार = 3 × परिमाप
= 3 × 128
Ans. 384 मीटर
Q.4 यदि समचतुर्भुज की एक भुजा और एक विकर्ण की लम्बाई क्रमशः 5 सेंटीमीटर और 8 सेंटीमीटर हैं तो उसका क्षेत्रफल हैं?
A. 13
B. 20
C. 24
D. 30
हल:- प्रश्नानुसार,
AC = 8 सेंटीमीटर
AO = 4 सेंटीमीटर
समकोण ∆AOB में,
BO = √5² – 4²
= √25 – 16
= √9
= 3 सेंटीमीटर
BD = 2 × 3
= 6 सेंटीमीटर
समचतुर्भुज का क्षेत्रफल = ½ × 6 × 8
= 24
Ans. 24 वर्ग सेंटीमीटर
Q.5 यदि किसी व्रत की त्रिज्या में 50% कमी कर दी जाए तो उसका क्षेत्रफल कम होगा?
A. 25%
B. 20%
C. 75%
D. 100%
हल:- प्रश्नानुसार,
माना कि वृत्त की त्रिज्या = r
क्षेत्रफल = πr²
नए वृत्त की त्रिज्या = r/2
क्षेत्रफल = π r²/4
= (π r² – π r²/4)/πr² × 100
= 75%
Ans. 75%
Q.6 यदि किसी वृत्त की त्रिज्या में 100% की वृद्धि की जाए, तो उसके क्षेत्रफल में कितने प्रतिशत की वृद्धि होगी?
A. 200%
B. 300%
C. 400%
D. 900%
हल:- प्रश्नानुसार,
माना त्रिज्या = a
क्षेत्रफल = πa²
वृद्धि के बाद त्रिज्या = 2a
क्षेत्रफल = 4πa²
% वृद्धि = 3πa²/πa² × 100
= 300%
Q.7 एक आयत का क्षेत्रफल 252 वर्ग सेंटीमीटर हैं। इसकी लम्बाई तथा चौड़ाई 9 : 7 हैं, इसका परिमाप क्या हैं?
A. 87 सेंटीमीटर
B. 56 सेंटीमीटर
C. 87 सेंटीमीटर
D. 64 सेंटीमीटर
हल:- आयत का क्षेत्रफल = 252
लम्बाई = 9
चौड़ाई = 7
9x × 7x = 252
63x² = 252
x² = 4
x = 2
9 × 2 = 18
7 × 2 = 14
आयत का परिमाप = 2(l + b)
= 2(18 + 14)
= 2 × 32
= 64
Ans. 64 सेंटीमीटर।
Q.8 75 किसी पहिए का व्यास 3 मीटर हैं। यह पहिया एक मिनट में 28 चक्कर लगाता हैं। 5.280 किलोमीटर की दूरी चलने में यह पहिया निम्न समय लेगा?
A. 10 मिनट
B. 20 मिनट
C. 30 मिनट
D. 40 मिनट
हल:- प्रश्नानुसार,
पहिए की परिधि = 3 × 22/7
= 66/7 मीटर
1 मिनट में चली दूरी = 66/7 × 28
= 264 मीटर
5.280 किलोमीटर में लगा समय
= 5280 मीटर/264 मीटर/मिनट
= 20 मीटर
Ans. 20 मीटर
उम्मीद हैं आपको चतुर्भुज की जानकारी पसंद आयी होगीं।
यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ शेयर कीजिए।
यदि आप इस पोस्ट से सम्बंधित कोई प्रश्न पूछना चाहते हैं तो कमेंट में जरूर पूछें धन्यवाद।