इस पेज पर आप Class 10th Maths Solutions Chapter 2 Ex 2.3 की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए चलिए पढ़ना शुरू करते हैं।
Chapter 2 : बहुपद : एक्साइज – 2.3
प्रश्न 1. विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए?
(i). p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii). p(x) = x⁴ – 3x² + 4x + 5,g (x) = x² + 1 – x
(iii). p(x) = x⁴ – 5x + 6, g (x) = 2 – x²
(i). p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
हल:- p(x) = x³ – 3x² + 5x – 3 एवं g(x) = x² – 2
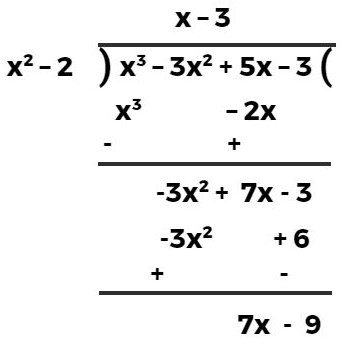
अतः अभीष्ट भागफल = x – 3 एवं शेषफल = 7x – 9 है।
(ii). p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
हल:- p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
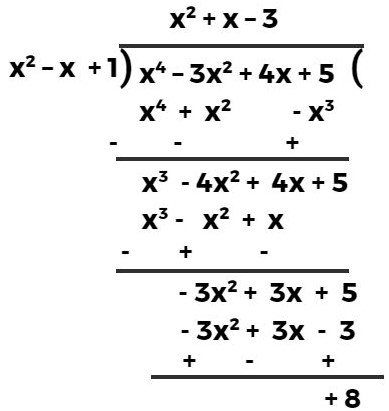
अतः अभीष्ट भागफल = x² + x – 3 एवं शेषफल = 8 है।
(iii). p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
हल:- p(x) = x⁴ – 5x + 6, g(x) = – x² + 2
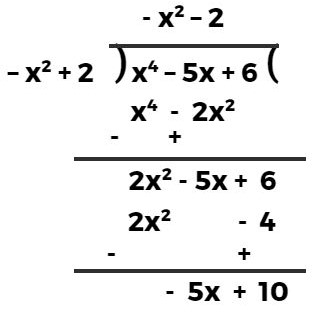
अतः अभीष्ट भागफल = -x² – 2 एवं शेषफल = -5x + 10 है।
प्रश्न 2. पहले बहुपद से दूसरे बहुपद को भाग करके जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखण्ड है?
(i). t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
हल:- यहाँ भाजक t² – 3 एवं भाज्य 2t⁴ + 3t³ – 2t² – 9t – 12 हैं जो मानक रूप में व्यवस्थित हैं।
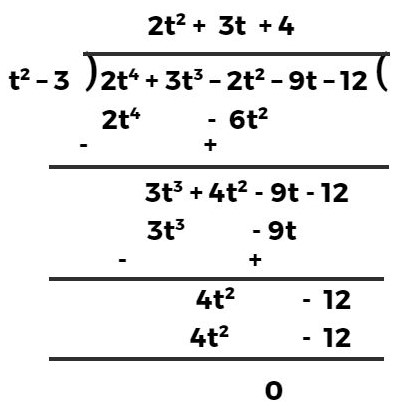
चूँकि यहाँ शेषफल शून्य आया है।
अतः, दिया हुआ प्रथम बहुपद, द्वितीय बहुपद का एक गुणनखण्ड है।
(ii). x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
हल:- यहाँ भाजक x² + 3x + 1 तथा भाज्य 3x⁴ + 5x³ – 7x² + 2x + 2 हैं जो मानक रूप में व्यवस्थित हैं।
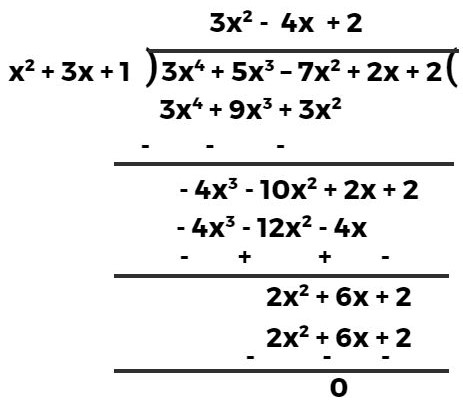
चूँकि यहाँ शेषफल शून्य आया है।
अतः, दिया हुआ प्रथम बहुपद द्वितीय बहुपद का एक गुणनखण्ड है।
(iii). x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
हल:- यहाँ भाजक x³ – 3x + 1 एवं भाज्य x⁵ – 4x³ + x² + 3x + 1 हैं जो मानक रूप में व्यवस्थित हैं।
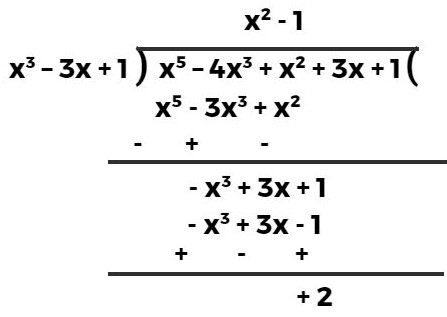
यहाँ शेषफल 2 आया है, शून्य नहीं है।
अतः, दिया हुआ प्रथम बहुपद, द्वितीय बहुपद का एक गुणनखण्ड नहीं है।
प्रश्न 3. 3x⁴ + 6x³ – 2x² – 10x – 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक √5/3 और -√5/3 हैं।
हल:- चूँकि √5/3 और -√5/3 दिए गए बहुपद के दो शून्यक हैं, इसलिए (x – √5/3)(x + √5/3) अर्धात (x² – 5/3) दिए गए बहुपद का एक गुणक होगा।
अब विभाजन एल्गोरिथ्म का प्रयोग दिए गए बहुपद एवं (x2 – 53) के लिए करते हैं।
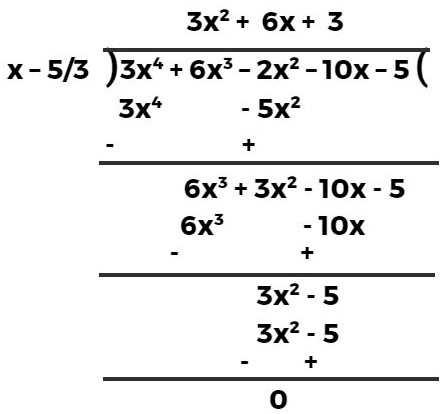
इसलिए 3x⁴ + 6x³ – 2x² – 10x – 5 = (x² – 5/3) (3x² + 6x + 3)
अब 3x² + 6x + 3 के गुणनखण्ड 3 (x + 1)² प्राप्त होते हैं इसलिए इसके शून्यक x = -1 एवं x = -1 होंगे।
अतः दिए बहुपद के अन्य शून्यक -1 और -1 है।
प्रश्न 4. यदि x³ – 3x² + x + 2 को एक बहुपद g(x) से भाग देने पर भागफल और शेषफल क्रमशः x – 2 और – 2x + 4 हैं, तो g (x) का मान ज्ञात कीजिए।
हल:- यूक्लिड की विभाजन प्रमेयिका का प्रयोग करने पर हम पाते हैं:
g (x).(x – 2) + (-2x + 4) = x³ – 3x² + x + 2
⇒ g (x).(x – 2) x³ – 3x² + x + 2 + 2x – 4
x³ – 3x² + 3x – 2
⇒ g(x) = 𝑥³−3𝑥² +3𝑥−2𝑥−2
इसलिए g (x) का मान ज्ञात करने के लिए हम बहुपद x³ – 3x² + 3x – 2 को व्यंजक x – 2 से विभाजित करेंगे
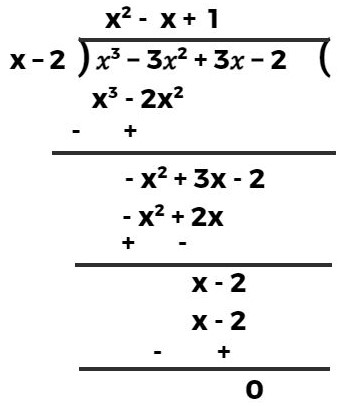
अतः g (x) का अभीष्ट मान x² – x + 1 है।
प्रश्न 5. बहुपदों p (x), g (x), q (x) और r (x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को सन्तुष्ट करते हों तथा
(i). घात p (x) = घात q(x)
हल:- p(x) = 2x² – 2x + 14, g (x) = 2,
q(x) = x² – x + 7 एवं r (x) = 0
(ii). घात q (x) = घात r (x)
हल:- p(x) = x³ + x² + x + 1, g (x) = x² – 1,
q(x) = x + 1 एवं r (x) = 2x +2
(iii). घात r (x) = 0
हल:- p(x) = x³ + 2x² – x + 2, g (x) = x2 – 1,
q(x) = x + 2 एवं r (x) = 4
ज्ञातव्य : उपर्युक्त तीनों प्रश्नों (i), (ii) एवं (iii) के अनेक उदाहरण हो सकते हैं।
जरूर पढ़िए :
उम्मीद हैं आपको Class 10th Maths Solutions Chapter 2 Ex 2.3 की पोस्ट पसंद आयी होगीं।
