इस पेज पर आप Class 10th Maths Solutions Chapter 3 Ex 3.1 की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए चलिए पढ़ना शुरू करते हैं।
Chapter 3 : दो चरों वाले रैखिक समीकरण : एक्साइज – 3.1
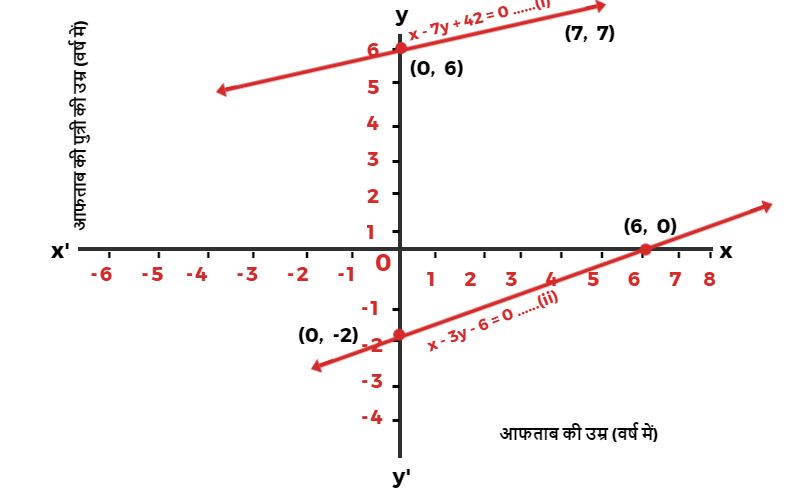
प्रश्न 1. आफताब अपनी पुत्री से कहता है सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा। इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए?
हल:- मान लीजिए कि आफताब एवं उसकी पुत्री की वर्तमान आयु क्रमशः x वर्ष और y वर्ष है, तो
प्रश्नानुसार,
(x – 7) = 7 (y – 7)
⇒ x – 7 = 7y – 49
⇒ x + 49 – 7 = 7y
⇒ x + 42 = 7y
⇒ y = (x + 42)/7………………….(i)
एवं (x + 3)= 3 (y + 3)
⇒ x + 3 = 3y + 9
⇒ x = 3y + 9 – 3
⇒ x = 3y + 6…………………….(ii)
समीकरण (ii) से x का मान समीकरण (i) में रखने पर
y = (x + 42)/7
y = (3y + 6 + 42)/7
y = (3y + 48)/7
7y = 3y + 48
7y – 3y = 48
4y = 48
y = 48/4
y = 12
y का मान समीकरण (ii) में रखने पर
x = 3y + 6
x = 3 × 12 + 6
x = 36 + 6
x = 42
समीकरण (i) से
y = (x + 42)/7
x = -7 रखने पर
y = (x + 42)/7
y = (- 7 + 42)/7
y = 35/7
y = 5
x = -7, y = 5
इसी प्रकार,
x = 0, y = 6
x = 7, y = 7
समीकरण (ii) से
x – 3y – 6 = 0
x = 6
x – 3y – 6 = 0
6 – 3y – 6 = 0
y = 0
इसी प्रकार,
x = 3, y = -1
x = 0, y = -2
| x | -7 | 0 | 7 |
| y | 5 | 6 | 7 |
| x | 6 | 3 | 0 |
| y | 0 | -1 | -2 |
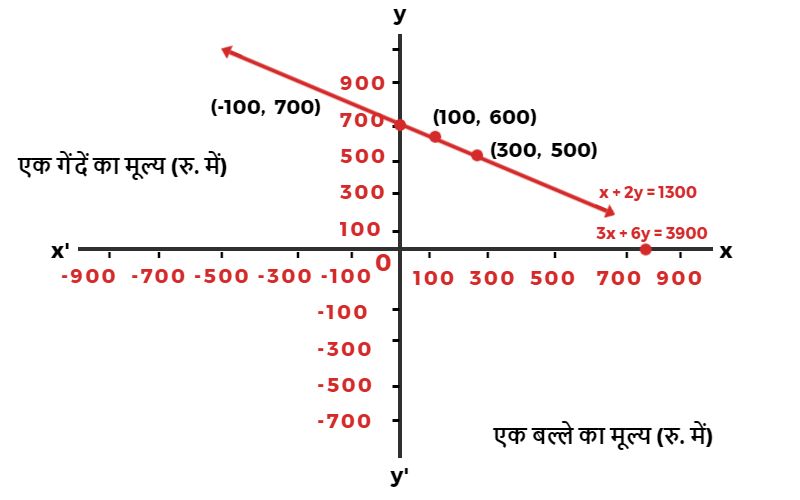
प्रश्न 2. क्रिकेट टीम के एक कोच ने ₹ 3900 में 3 बल्ले तथा 6 गेंदें खरीदी। बाद में उसने एक और बल्ला तथा उसी प्रकार की 3 गेंदें ₹ 1300 में खरीदीं। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए?
हल:- माना, 1 बल्ले एवं 1 गेंद का मूल्य क्रमशः ₹ x तथा ₹ y है।
प्रश्नानुसार,
3x + 6y = 3900 ……………(i)
समीकरण (i) में 3 से भाग देने पर
x + 2y = 1300 ……………(ii)
समीकरण (ii) में x = 300 रखने पर
x + 2y = 1300
300 + 2y = 1300
2y = 1300 – 300
2y = 1000
y = 500
इसी प्रकार,
x = 100, y = 600
x = -100, y = 700
| x | 300 | 100 | -100 |
| y | 500 | 600 | 700 |
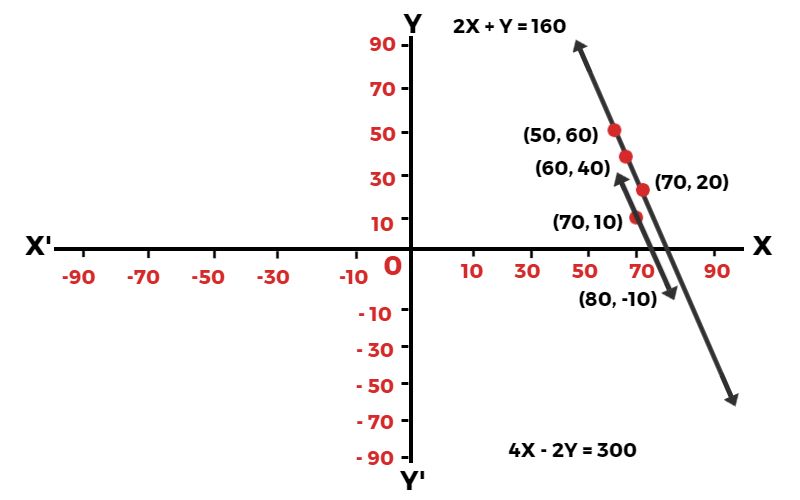
प्रश्न 3. 2 kg सेब और 1 kg अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 kg सेब और 2 kg अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए?
हल:- मान 1 किलो सेब एवं 1 किलो अंगूर का मूल्य क्रमश: ₹ x एवं ₹ y है।
प्रश्नानुसार,
2x + y = 160 …………….(i)
एवं 4x + 2y = 300
⇒ 2x + y = 150 ………..(ii)
अतः दी गई स्थितियों का बीजगणितीय निरूपण है
2x + y = 160
2x + y = 150
ज्यामितीय (ग्राफीय) निरूपण के लिए
2x + y = 160
y = 160 – 2x
समीकरण (i) में x = 50 रखने पर
2x + y = 160
2 × 50 + y = 160
100 + y = 160
y = 160 – 100
y = 60
इसी प्रकार,
x = 60, y = 40
x = 70, y = 20
| x | 50 | 60 | 70 |
| y | 60 | 40 | 20 |
2x + y = 150………………(ii)
समीकरण (ii) में x = 70 रखने पर
2x + y = 150
2 × 70 + y = 150
140 + y = 150
y = 150 – 140
y = 10
इसी प्रकार,
x = 80, y = -10
x = 75, y = 0
| x | 70 | 80 | 75 |
| y | 10 | -10 | 0 |
जरूर पढ़िए :
- Class 10th Maths Solutions Chapter 2 Ex 2.1
- Class 10th Maths Solutions Chapter 2 Ex 2.2
- Class 10th Maths Solutions Chapter 2 Ex 2.3
उम्मीद हैं आपको Class 10th Maths Solutions Chapter 3 Ex 3.1 की पोस्ट पसंद आयी होगीं।
