इस पेज पर आप गणित के महत्वपूर्ण अध्याय ऊँचाई एवं दूरी को पड़ेगें।
पिछले पेज पर हमने अनुपात और समानुपात की जानकारी शेयर की उसे भी पढ़े।
चलिए आज हम ऊँचाई एवं दूरी की जानकारी पढ़ते और समझते हैं।
Table of Contents
ऊँचाई की परिभाषा
किसी भी वस्तु की लम्बवत दिशा में माप ऊँचाई कहलाती हैं।
जैसे हमारी ऊँचाई 5 फुट 3 इंच, 5 फुट 6 इंच या 6 फुट कुछ भी हो सकती हैं इसी प्रकार किसी भी वस्तु की ऊपर से नीचे तक के माप को ऊँचाई कहते हैं।
दूरी की परिभाषा
एक वस्तु से दूसरी वस्तु के बीच के अंतर को दूरी कहते हैं।
जैसे यदि कोई वस्तु एक निश्चित बिंदु से 1000 मीटर दूर हैं या 1 किलोमीटर दूर है या बम्बई से दिल्ली की दूरी हो उसे दूरी कहाँ जाता हैं।
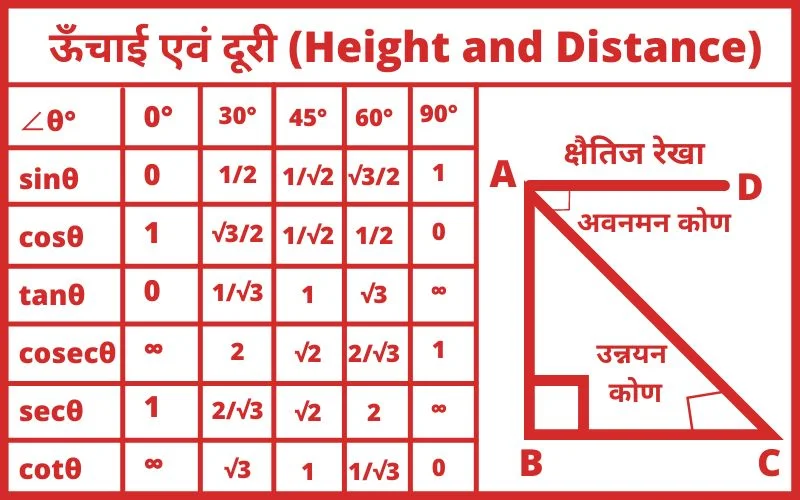
उन्नयन कोण एवं अवनमन कोण
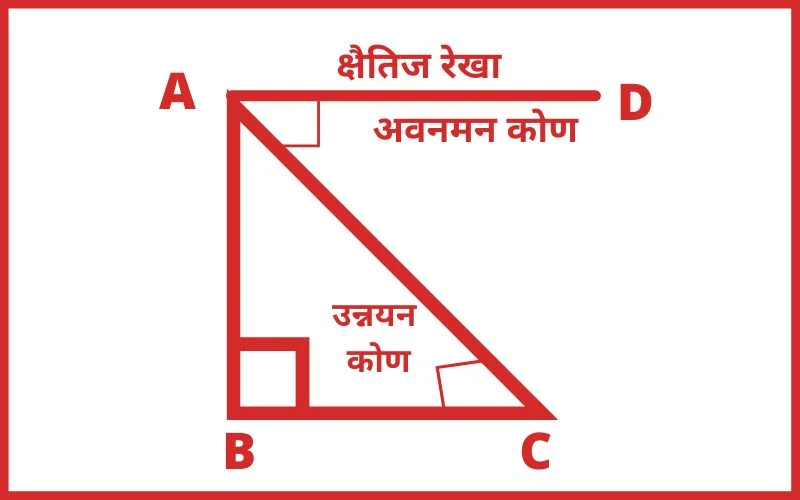
माना,
कि A कोई वस्तु हैं जिनको देखना हैं और देखनेवाले की आँख की स्थिति C हैं AC रेखा को A बिंदु की दृष्टि रेखा कहते हैं।
C बिंदु से B तक खिंची गई रेखा एक क्षैतिज रेखा हैं जो उस ऊर्ध्वाधर समतल में हैं जिसमें CA स्थित हैं।
∠BCA जो दृष्टि रेखा CA और क्षैतिज रेखा CB के बीच में हैं।
A उन्नयन कोण कहलाता हैं।
∠DAC जो दृस्टि रेखा AC और क्षैतिज रेखा DA के बीच में हैं।
C का अवनमन कोण कहलाता हैं।
ऊँचाई एवं दूरी से संबंधित प्रश्नों को हल करने के लिए sinθ, cosθ, tanθ, cosecθ, secθ, cotθ का मान अलग-अलग कोण के लिए जरुरी हैं जो चलिए नीचे दिए मानों को पढ़ते हैं।
| ∠θ° | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sinθ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| cosθ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tanθ | 0 | 1/√3 | 1 | √3 | ∞ |
| cosecθ | ∞ | 2 | √2 | 2/√3 | 1 |
| secθ | 1 | 2/√3 | √2 | 2 | ∞ |
| cotθ | ∞ | √3 | 1 | 1/√3 | 0 |
ऊँचाई और दूरी के सवाल
Q.1 सूर्य का उन्नयन कोण ज्ञात कीजिए जबकि एक छड़ी की छाया उसकी लम्बाई की √3 गुनी हैं?
A. 45°
B. 60°
C. 30°
D. 90°
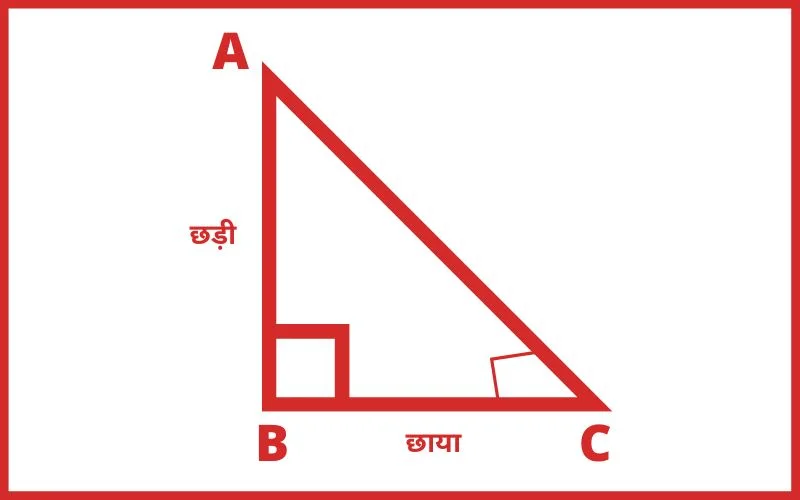
हल: माना,
उन्नयन कोण = θ
प्रश्ननानुसार,
BC = √3 × AB ………(1)
समकोण त्रिभुज ABC से,
tanθ = लम्ब/आधार
tanθ = AB/BC
समीकरण (1) से
tanθ = AB/√3 × AB
tanθ = 1/√3
tanθ = tan30°
θ = 30°
Ans. 30°
Q.2 एक डोरी की पतंग से भूमि के किसी बिंदु तक दूरी 90 मीटर हैं डोरी भूमितल के साथ 60° का कोण बनाती हैं यह मानते हुए की डोरी में कोई डील नहीं हैं, पतंग की ऊँचाई निकालिए?
A. 45√3
B. 60√3
C. 45 मीटर
D. 60 मीटर
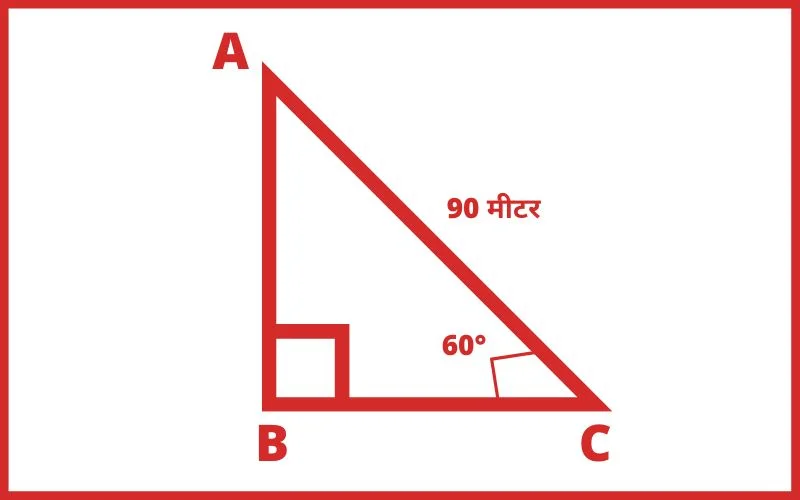
हल: माना,
पतंग की ऊँचाई BA = h मीटर
सनकोण त्रिभुज ABC में
sin60° = लम्ब/कर्ण
sin60° = AB/AC
√3/2 = h/90
2h = 90√3
h = 90√3/2
h = 45√3
पतंग की ऊँचाई 45√3 मीटर होगी।
Ans. 45√3
Q.3 एक पतंग की डोरी 100 मीटर लम्बी हैं यदि डोरी एक सरल रेखा के रूप में हो एवं भू-तल के साथ θ कोण इस प्रकार बनाती है कि sinθ = 8/15, तो भू-तल से पतंग की ऊँचाई निकालें
A.107/2 मीटर
B. 53½ मीटर
C. 54 मीटर
D. 101/2 मीटर
हल: समकोण त्रिभुज ABC में,
Sinθ = लम्ब/कर्ण
Sinθ = AB/AC
8/15 = AB/100
15 AB = 100 × 8
AB = (100 × 8)/15
AB = 160/3 मीटर
अतः भू-तल में पतंग की ऊँचाई = 53½ मीटर
Ans. 53½ मीटर
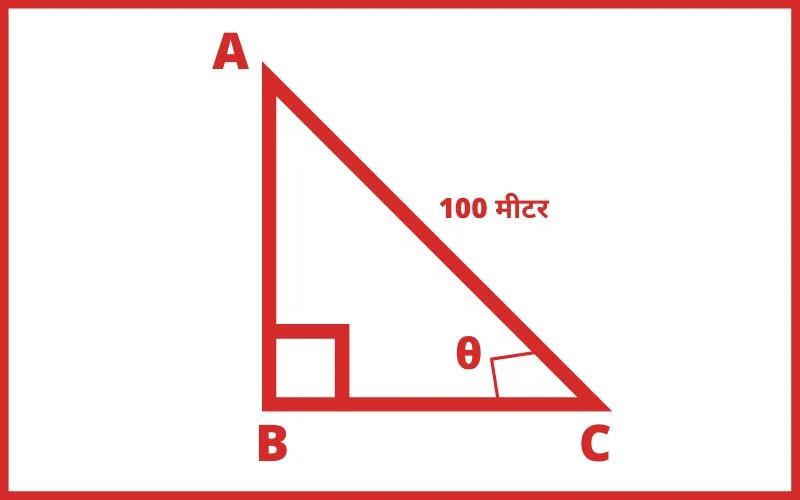
Q.4 100 मीटर किमी. रस्ती को किसी टॉवर के शीर्ष और पृथ्वी पर बिंदु के बीच बाधा जाता हैं, यदि रस्सी बिना किसी तार के सहारे हैं और समतल के साथ 60° का कोण बनाती हैं, तो टॉवर की ऊँचाई क्या हैं?
A. 60 मी.
B. 50 मी.
C. 86.60 मी.
D. 66.7 मी.
हल: माना,
टॉवर AB की ऊँचाई h मीटर हैं
तब, sin60° = लम्ब/कर्ण
sin60° = AB/AC
sin60° = h/100
√3/2 = h/100
2h = 100√3
h = 100√3/2
h = 50√3
h = 50 × 1.732
h = 86.600
Ans. 86.60 मीटर
Q.5 जब सूर्य क्षितिज से 30° ऊपर हो, तो 50 मीटर ऊँचे किसी भवन द्वारा डाली गई परछाई की लंबाई हैं?
A. 50√3
B. 25 मीटर
C. 25√3
D. 50/√3
हल: ∆ABC में,
cot30° = आधार/लम्ब
cot30° = BC/AB
√3 = x/50
x = 50√3 मीटर
Ans. 50√3 मीटर
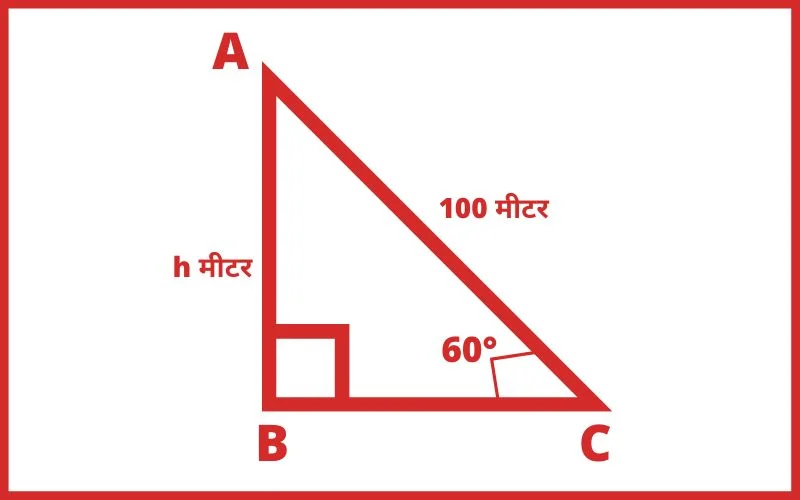
Q.6 एक समतल मैदान पर बिंदु P से एक टॉवर के शीर्ष के एलिवेशन का कोण 30° है यदि टॉवर की ऊँचाई 100 मीटर हैं तो बिंदु P की टॉवर के पैरों से लगभग दूरी होगी?
A. 200 मीटर
B. 173 मीटर
C. 156 मीटर
D. 149 मीटर
हल: माना,
बिंदु p की टॉवर AB के पाद से दूरी = x मीटर
cot30° = आधार/लम्ब
cot30° = BP/AB
√3 = x/100
x = 100√3
x = 100 × 1.732
x = 173 मीटर
Ans. 173 मीटर
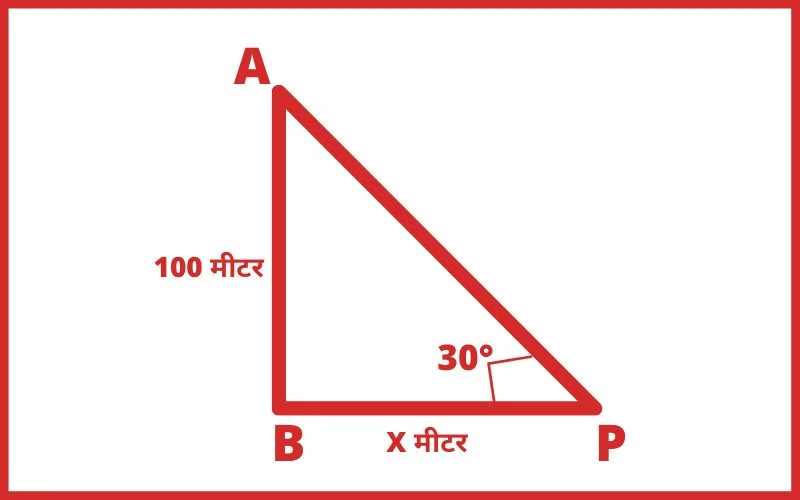
Q.7 एक वृक्ष के आधार से 15 मीटर दूर स्थित बिंदु पर उसकी चोटी का उन्नयन कोण 30° है, तो वृक्ष की ऊँचाई होगी?
A. 30 मीटर
B. 15√3 मीटर
C. 30√3 मीटर
D. 5√3 मीटर
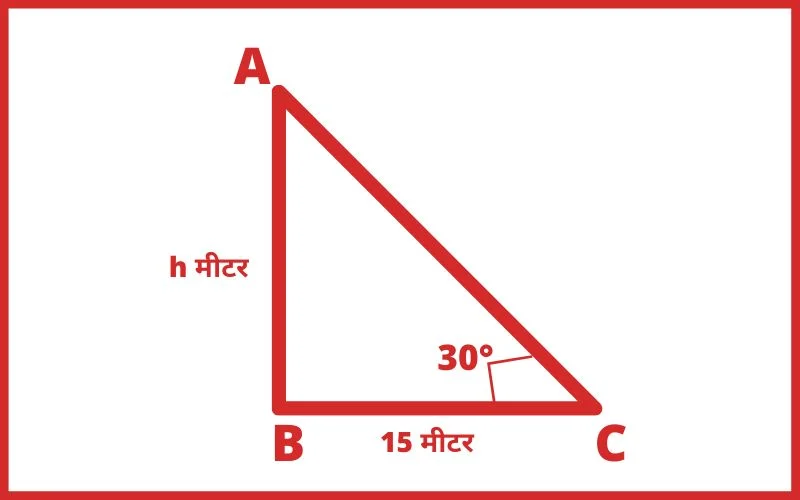
हल: माना,
वृक्ष की ऊँचाई = h मीटर
∆ABC में,
tan30° = लम्ब/आधार
1/√3 = AB/BC
1/√3 = h/15
√3h = 15
h = 15/√3
h = 15/√3
h = 15 × √3/√3 × √3
h = 15√3/3
h = 5√3
Ans. 5√3 मीटर
Q.8 हवा के झोंके से एक पेड़ का ऊपरी भाग टूटकर 2√3 मीटर की दूरी पर 60° के कोण पर जमीन को छूता है, तो पेड़ की ऊँचाई क्या हैं?
A. 12.928 मीटर
B. 11 मीटर
C. 12 मीटर
D. 10 मीटर
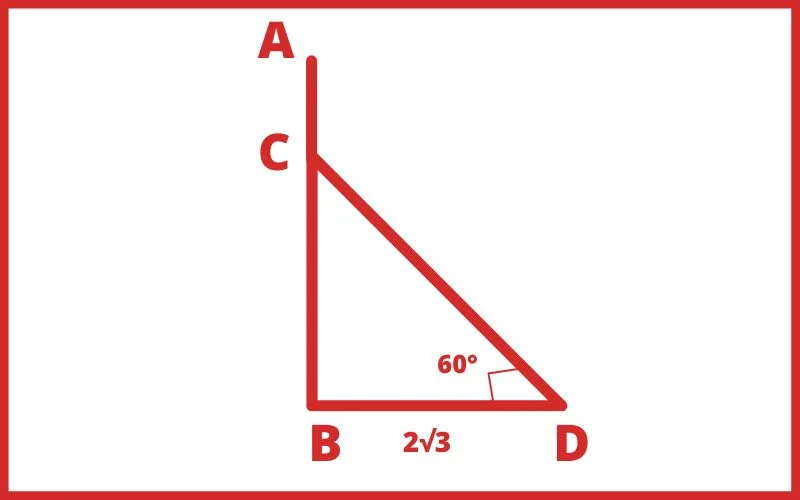
हल: ∆CBD में,
cos60° = आधार/कर्ण
cos60° = BD/CD
1/2 = 2√3/CD
CD = 4√3 = AC
tan60° = BC/BD
√3 = BC/2√3
BC = 2 × 3
BC = 6 मीटर
पेड़ की ऊँचाई = (4√3+6) मीटर
12.928 मीटर
Ans. 12.928 मीटर
Q.9 20 मीटर ऊँची एक मीनार पर एक झंडा गड़ा हैं, जमीन पर स्थित एक बिंदु से झंडे के खंभे के पाद और शीर्ष के उन्नयन कोण क्रमशः 45° और 60° है, तो झंडे के खंभे की लम्बाई क्या हैं?
A. 20(√3 – 1) मीटर
B. 20(3 + √3) मीटर
C. 20(√3 + 1) मीटर
D. 20(3 – √3) मीटर
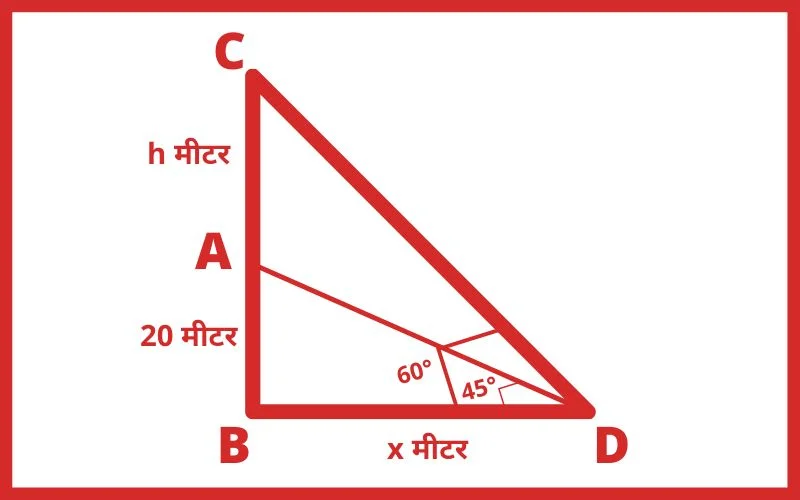
हल: माना,
झण्डे के खम्भे AC की लंबाई = h मीटर तथा BD = x मीटर
∆ABD में,
tan45° = AB/BD
1 = 20/x
x = 20
∆CBD में,
tan60° = BC/BD
√3 = (20 + h)/20
20√3 = 20 + h
h = 20√3 – 20
h = 20(√3 – 1) मीटर
Ans. 20(√3 – 1) मीटर
Q.10 एक मीनार पर 10 मीटर लम्बा एक झण्डा खड़ा हैं जमीन पर स्थित एक बिंदु से झण्डे के पाद और शीर्ष के उन्नयन कोण क्रमशः 30° और 60° है, तो मीनार की ऊँचाई क्या हैं?
A. 10 मीटर
B. 5 मीटर
C. 15 मीटर
D. 20 मीटर
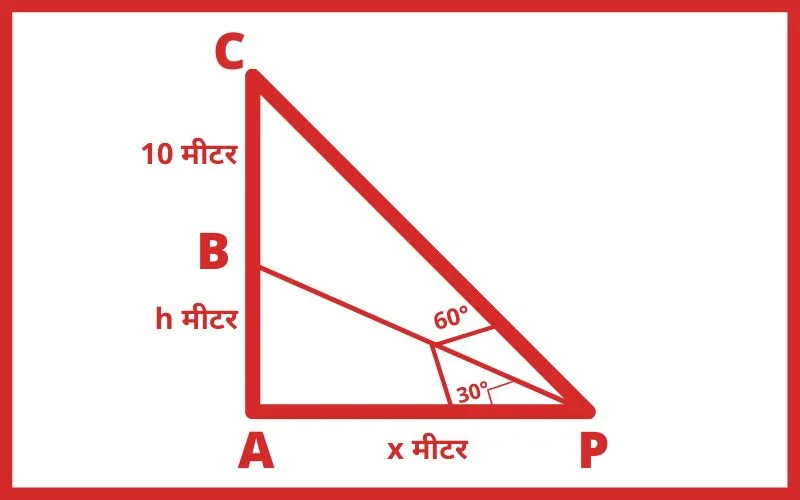
हल: माना,
मीनार AB की ऊँचाई = h मीटर, तथा AP = x मीटर, झंडा BC = 10 मीटर,
∆PAB में,
tan30° = AB/AP
1/√3 = h/x
x = √3h …….(1)
∆PAC में,
tan60° = AC/AP
√3 = (h + 10)/x
√3x = h + 10
समीकरण (1) से x का मान रखने पर,
√3 × √3h = h + 10
3h = h + 10
3h – h = 10
2h = 10
h = 5
Ans. 5
Q.11 9 मीटर लम्बी सीढ़ी एक उर्ध्वधर ध्वज्दण्ड के शीर्ष से 9 मीटर नीचे तक पँहुचाती है ध्वजदंड के शीर्ष का सीढ़ी के निचले सिरे के उन्नयन कोण 60° है ध्वजदण्ड की ऊँचाई क्या हैं?
A. 12 मीटर
B. 13 मीटर
C. 13.5 मीटर
D. 14 मीटर
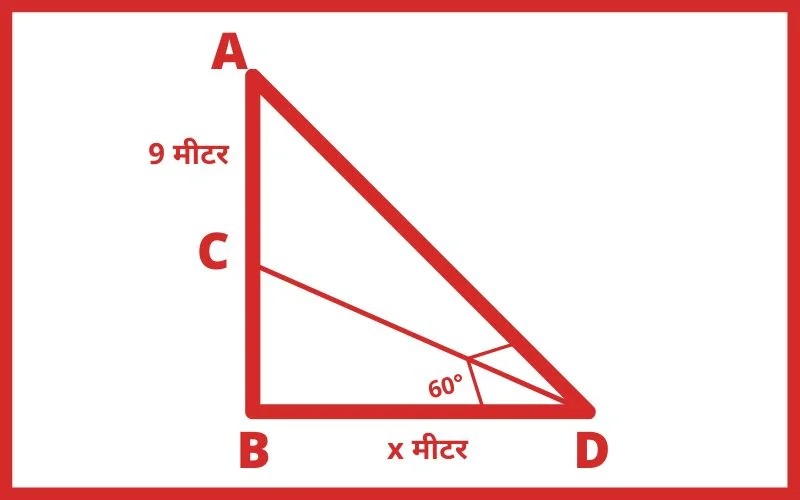
हल: ∠A = 90° – 60°
∠A = 30°
∠CDB = 60° – 30°
∠CDB = 30°
∠CDB में,
sin30° = लम्ब/कर्ण
sin30° = BC/CD
1/2 = CB/CD
1/2 = CB/9
CB = 9/2 मीटर
अतः ध्वजदण्ड की ऊँचाई = AB
AB = (9 + 9/2) मीटर
AB = 13.5 मीटर
Ans. 13.5 मीटर
Q.12 दो ट्रेनें चंडीगढ़ के लिए दिल्ली से शाम 6 बजे और शाम 6.30 बजे चलती हैं और उनकी चाल क्रमशः 60 किलोमीटर/घण्टा और 75 किलोमीटर/घण्टा हैं दिल्ली से कितने किलोमीटर दूरी पर वे दोनों ट्रेन की मिलन होंगी?
A. 67.5
B. 150
C. 75
D. 60
हल:- प्रश्नानुसार,
पहली रेलगाड़ी के द्वारा आधे घण्टे में तय की गई दूरी = 60 × 1/2
दूरी = 30 किलोमीटर
सापेक्षिक गति = (75 – 60) किलोमीटर/घण्टा
= 75 किलोमीटर/घण्टा
मिलने में लगा समय = 30/15 = 2 घण्टे
अभीष्ट दूरी = 75 × 2
अभीष्ट दूरी = 150 किलोमीटर
Ans. 150 किलोमीटर
Q.13 एक 130 मीटर लम्बी रेलगाड़ी एक पुल को 90 किलोमीटर/घण्टा की गति से चलते हुए 21 सेकेण्ड में पार करती हैं तो पुल की लम्बाई होंगी?
A. 285 मीटर
B. 395 मीटर
C. 295 मीटर
D. 415 मीटर
हल:- प्रश्नानुसार,
पुल की लम्बाई = (90 × 5/18 × 21) – 130
= (5 × 5 × 21) – 130
= 525 – 130
= 395
Ans. 395 मीटर
Q.14 एक रेलगाड़ी नई दिल्ली रेलवे स्टेशन से 9 बजे सुबह 45 किलोमीटर/घण्टा की गति से चलती हैं एक अन्य रेलगाड़ी नई दिल्ली रेलवे स्टेशन से उसी दिशा में 12 बजे दोपहर 60 किलोमीटर/घण्टा की गति से जाती हैं नई दिल्ली रेलवे स्टेशन से उस स्थान की दूरी जहाँ दोनों गाड़ियों का मेल होगा?
A. 60 किलोमीटर
B. 360 किलोमीटर
C. 450 किलोमीटर
D. 540 किलोमीटर
हल:- प्रश्नानुसार,
Tricks :
समय = 45(12 – 9)/15
समय = (45 × 3)/15
समय = 3 × 3
समय = 9
दूरी = 9 × 60
दूरी = 540 किलोमीटर
Ans. 540 किलोमीटर
Q.15 टेलीग्राफ के खम्भे 50 मीटर की दूरी पर लगे हैं एक रेलयात्री जैसे ही उनके पास से निकलता हैं खम्भे गिनता हैं यदि गाड़ी की गति 45 किलोमीटर/घण्टा हैं, तो 4 घण्टे में कितने खम्भे निकल जाएंगे?
A. 360
B. 3000
C. 36000
D. 3600
हल:- प्रश्नानुसार,
4 घण्टे में तय की गई दूरी = 45 × 4
= 180 किलोमीटर
= 180000 मीटर
खम्भों की अभीष्ट संख्या = 180000/50
= 3600
Ans. 3600
Q.16 कोई ट्रेन एक स्टेशन से दूसरे तक जाने में 3 घण्टे का समय लेती हैं इसकी चाल यदि 12 किलोमीटर/घण्टा कम कर दी जाए तब इस यात्रा में उसे 45 मिनट अधिक लगते हैं स्टेशनों के बीच की दूरी हैं?
A. 220 किलोमीटर
B. 210 किलोमीटर
C. 180 किलोमीटर
D. 160 किलोमीटर
हल:- माना कि स्टेशनों के बीच की दूरी = x किलोमीटर
ट्रैन की प्रारंभिक गति = x/3 किलोमीटर/घण्टा
परिणामी गति = (x/3 – 12) किलोमीटर/घण्टा
प्रश्नानुसार,
(x/3 – 12) 15/4 = x
x/3 – 12 = 4x/15
(x – 36)/3 = 4x/15
x – 36 = 4x/5
5 (x – 36) = 4x
5x – 180 = 4x
5x – 4x = 180
x = 180
Ans. 180
जरूर पढ़िए :
उम्मीद हैं आपको ऊँचाई एवं दूरी की जानकारी पसंद आयी होगीं।
यदि आपको ऊँचाई एवं दूरी की पोस्ट पसंद आयी हो तो दोस्तों के साथ जरूर शेयर करें।
ऊँचाई एवं दूरी से सम्बन्धित किसी भी प्रश्न के लिए कमेंट करें।