द्विआधारी पद्धति की परिभाषा, प्रकार और उदाहरण

इस पेज पर आप बाइनरी नंबर सिस्टम या द्विआधारी पद्धति प्रणाली की सम्पूर्ण जानकारी पड़ेगें।

पिछले पेज पर हमने संख्या पद्धति की समस्त जानकारी शेयर की हैं तो इस पोस्ट को भी पढ़े।

चलिए इस पेज पर बाइनरी नंबर सिस्टम (Binary Number System) की जानकारी पढ़ते और समझते हैं।

द्विआधारी पद्धति प्रणाली क्या हैं

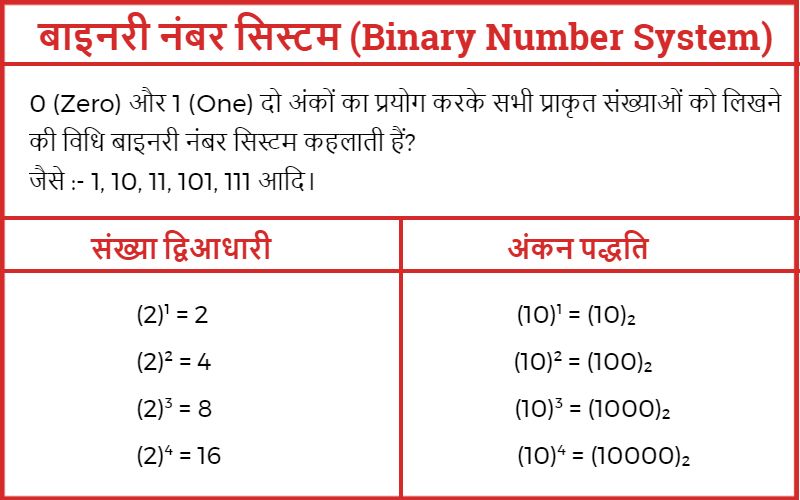
0 (Zero) और 1 (One) दो अंकों का प्रयोग करके सभी प्राकृत संख्याओं को लिखने की विधि बाइनरी नंबर सिस्टम या द्विआधारी संख्या प्रणाली कहलाती हैं?

जैसे :- 1, 10, 11, 101, 111 आदि।

द्विआधारी पद्धति में 2 को आधार माना जाता हैं। द्विआधारी अंकन पद्धति में 2 को 10 लिखते हैं और शेष संख्याओं का निर्माण भी 10 के ही आधार पर होता हैं।

जैसे :-

द्विआधारी संख्या	अंकन पद्धति
(2)¹ = 2	(10)¹ = (10)₂
(2)² = 4	(10)² = (100)₂
(2)³ = 8	(10)³ = (1000)₂
(2)⁴ = 16	(10)⁴ = (10000)₂

अब इसके अतिरिक्त संख्याएँ 3, 5, 6, 7, 9, 10, 11 को उपरोक्त के आधार पर बहुत आसानीपूर्वक द्विआधारी पद्धति में व्यक्त करते हैं।

जैसे :-

(¡). 3 = 2 + 1 → 10 + 1 = (11)₂
(ii). 5 = 4 + 1 → 100 + 1 = (101)₂
(¡¡¡). 6 = 4 + 2 → 100 + 10 = (110)₂
(iv). 7 = 4 + 2 + 1 → 100 + 10 + 1 = (111)₂
(v). 9 = 8 + 1 → 1000 + 1 = (1001)₂
(vi). 10 = 8 + 2 → 1000 + 10 = (1010)₂
(vii). 20 = 16 + 4 → 10000 + 100 = (10100)₂

अंकीय गिनती (Digital Counting)

2¹	2 . 1 = 2	2
2²	2. 2 = 4	4
2³	2 . 2 . 2 = 8	8
2⁴	2 . 2 . 2 . 2 = 16	16
2⁵	2 . 2 . 2 . 2 . 2 = 32	32
2⁶	2 . 2 . 2 . 2 . 2 . 2 = 64	64
2⁷	2 . 2 . 2 . 2 . 2 . 2 . 2 = 128	128
2⁸	2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 = 256	256
2⁹	2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 = 512	512
2¹⁰	2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 = 1024	1024
2²⁰	1024² = 1024 . 1024	10,48,576
2³⁰	1024³ = 1024. 1024 . 1024	10,73,741
2⁴⁰	1024⁴ = 1024. 1024 . 1024 . 1024	10,99,51,16,27,776
2⁵⁰	1024⁵ = 1024. 1024 . 1024 . 1024 . 1024	1,12,58,99,90,68,42,620

1 से 1000 तक गिनती की पोस्ट जरूर पढ़िए।

द्विआधारी गिनती (Counting in Binary)

दाशमिक संख्या	द्विआधारी पैटर्न
1	0
2	1
3	10
4	11
5	100
6	101
7	110
8	111
9	1000
10	1001
11	1010
12	1011
13	1100
14	1101
15	1110
16	1111
17	10000
18	10001
19	100010
20	100011

बाइनरी नंबर सिस्टम के प्रकार

बाइनरी नंबर सिस्टम के 4 प्रकार होते हैं।

• द्विआधारी संख्या प्रणाली
• ऑक्टल संख्या प्रणाली
• दशमलव संख्या प्रणाली
• हेक्साडेसिमल संख्या प्रणाली

1. द्विआधारी संख्या प्रणाली

द्विआधारी संख्या प्रणाली में केवल दो अंक ‘0‘ और ‘1‘ होते हैं। इस द्विआधारी संख्या प्रणाली को आधार नंबर सिस्टम भी कहते है क्योंकि द्विआधारी संख्या प्रणाली का आधार 2 है, इसमें केवल दो अंक हैं।

2. ऑक्टल संख्या प्रणाली

ऑक्टल संख्या प्रणाली में केवल आठ (8) अंक 0 से 7 होते हैं। प्रत्येक संख्या 0, 1, 2, 3, 4, 5, 6 और 7 के साथ इस नंबर प्रणाली में दर्शाती है इसका Base 8 होता है। ऑक्टल नंबर सिस्टम का आधार 8 है क्योंकि इसमें केवल 8 अंक हैं।

3. दशमलव संख्या प्रणाली

दशमलव संख्या प्रणाली में 0 से 9 तक केवल दस (10) अंक होते हैं। प्रत्येक संख्या इस संख्या प्रणाली में 0, 1, 2, 3, 4, 5, 6, 7, 8 और 9 के साथ दर्शाती है इसका Base 10 होता है। दशमलव संख्या प्रणाली का आधार 10 है, क्योंकि इसमें केवल 10 अंक हैं।

4. हेक्साडेसिमल संख्या प्रणाली

हेक्साडेसिमल संख्या प्रणाली में सोलह (16) अल्फ़ान्यूमेरिक मान 0 से 9 और A से F होते हैं। प्रत्येक नंबर 0, 1, 2, 3, 4, 5, 6, 7, 9, 9, A,B,C,D,E और F इस संख्या प्रणाली के साथ दर्शाता है इसका Base 16 होता है।

हेक्साडेसिमल संख्या प्रणाली का आधार 16 है, क्योंकि इसमें 16 अल्फ़ान्यूमेरिक मान हैं। यहां A = 10, B = 11, C = 12, D = 13, E = 14 और F 15 है।

बाइनरी नंबर सिस्टम पर आधारित प्रश्न

Q.1 (11011)₂ + (101)₂ का मान होगा?
A. 30
B. 31
C. 32
D. 33

हल :- प्रश्नानुसार,
(11011)₂ + (101)₂
1 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰ + 1 × 2² + 0 × 2¹ + 1 × 2⁰
16 + 8 + 0 + 2 + 1 + 4 + 1
32
Ans. 32

Q.2 (111)₂ + (11)₂ = ?
A. 1010
B. 1111
C. 11111
D. 1110

हल:- प्रश्नानुसार,
(111)₂ + (11)₂ = ?
100 +10 + 1 + 10 + 1 = ?
? ⇒ 4 + 2 + 1 + 2 + 1 = 10
? ⇒ 8 + 2 = 1000 + 10
? = 1010
Ans. 1010

Q.3 (11011)₂ – (101 )₂ का मान होगा?
A. 20
B. 21
C. 22
D. 23

हल:- प्रश्नानुसार,
(11011)₂ – (101 )₂
1 × 2⁴ + 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰− [1×2²+0×2+1×2⁰]
(16 + 8 + 2 + 1) − 5
27 − 5
22
Ans. 22

Q.4 (10001)₂ × (100)₂ = ?
A. 34
B. 35
C. 58
D. 68

हल:- प्रश्नानुसार,
(10001)₂ × (100)₂ = ?
(1 × 2⁴ + 0 + 0 + 0 + 1) × 4 = ?
(16 + 1) × 4 = ?
17 × 4 + ?
68 = ?
? = 68
Ans. 68

Q.5 (11001)₂ ÷ (101)₂ = ?
A. 5
B. 10
C. 15
D. 20

हल:- प्रश्नानुसार,
(11001)₂ ÷ (101)₂ = ?
(1 × 2⁴ + 1 × 2³ + 0 + 0 + 1)/(1 × 2² + 0 + 1) = ?
(16 + 8 + 1)/(4 +1) = ?
25/5 = ?
5 = ?
? = 5
Ans. 5

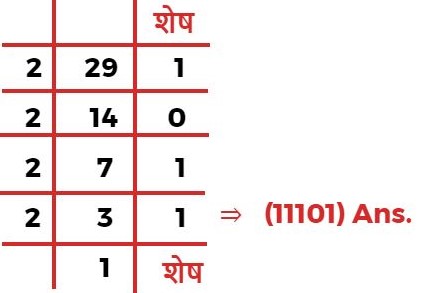
Q.6 29 द्विआधारी संख्या पद्धति में किस प्रकार लिखा जाएगा?
A. 11001
B. 11101
C. 10001
D. 1101

Q.7 129 को द्विआधारी संख्या पद्धति में व्यक्त करने पर कितने अंकों में लिखा जाएगा?
A. 7
B. 6
C. 8
D. 9

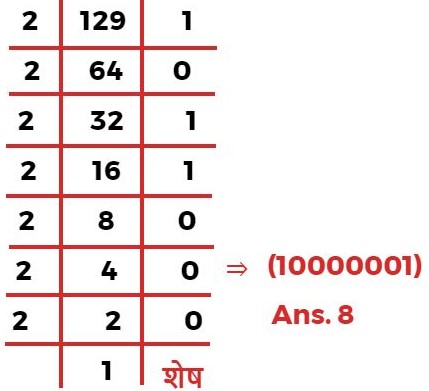
129 = 128 + 1
1 × 2⁷ + 1
अभीष्ट अंकों की संख्या = 7 + 1
संख्या = 8
Ans. 8

Q.8 (1011010)₂ को संख्या में परिवर्तित करें?
A. 84
B. 85
C. 90
D. 110

हल:- प्रश्नानुसार,
(1011010)₂
(1 × 2⁶ + 0 × 2⁵ + 1 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰)
64 + 0 + 16 + 8 + 0 + 2 + 0
90
Ans. 90

Q.9 (110)₂ को संख्या में परिवर्तित करें?
A. 10
B. 7
C. 5
D. 9

हल:- प्रश्नानुसार,
(110)₂
1 × 2² + 1 × 2¹ + 0 × 2¹
8 + 1
9
Ans. 9

Q.10 (110111)₂ × 2 = ?
A. 6
B. 5
C. 10
D. 16

हल:- प्रश्नानुसार,
(110111)₂ × 2 = ?
(1 × 2⁵ + 1 × 2⁴ + 0 + 1 × 2² + 1 × 2 + 1) × 2 = ?
(32 + 16 + 4 + 2 + 1) × 2 = ?
55 × 2 = ?
110 = ?
(110)₂ = 1 × 2² + 1 × 2 + 10
4 + 2 + 10 = 16
Ans. 16

Q.11 (11110)₂ का मान ज्ञात करें?
A. 20
B. 30
C. 22
D. 50

हल:- प्रश्नानुसार,
(11110)₂
1 × 2⁴ + 1 × 2³ + 1 × 2² + 1 × 2 + 0
16 + 8 + 4 + 2
30
Ans. 30

Q.12 (1101)₂ + (10011)₂ का मान द्विआधारी अंकन पद्धति में ज्ञात करें?
A. (110000)₂
B. (1000000)₂
C. (10000001)₂
D. (10000000)₂

हल:- प्रश्नानुसार,
(1101)₂ + (10011)₂
(1 × 2³ + 1 × 2² + 0 + 1) + (1 × 2⁴ + 0 + 0 + 0 + 2 + 1)
(8 + 4 + 1) + (16 + 3)
13 + 19 = 32
(2)⁵ = (10)⁵ = 100000
Ans. (100000)₂

FAQ

जरूर पढ़िए :

संख्या पद्धति
सरलीकरण
दशमलव भिन्न
आरोही क्रम और अवरोही क्रम

उम्मीद हैं आपको बाइनरी नंबर सिस्टम की पोस्ट पसंद आयी होगीं।

यदि आपको ये पोस्ट पसंद आयी हो तो अपने दोस्तों के साथ जरूर शेयर करें।