संख्या किसे कहते हैं संख्या के प्रकार और उदाहरण

इस पेज पर आप संख्या की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।

पिछले पेज पर हमने अंक की जानकारी शेयर की हैं जो गणित का आधार हैं उस पोस्ट को भी पढ़े।

चलिए इस पेज पर संख्याओं की समस्त जानकारी पढ़ते और समझते हैं।

संख्या किसे कहते हैं

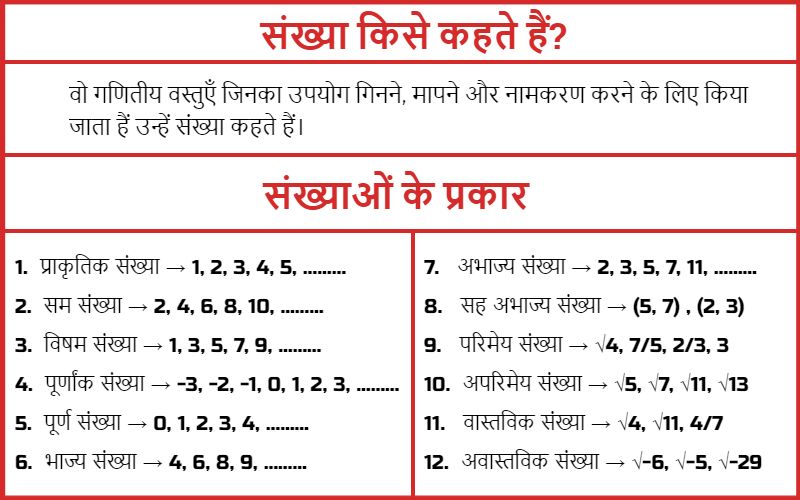
वो गणितीय वस्तुएँ जिनका उपयोग गिनने, मापने और नामकरण करने के लिए किया जाता हैं उन्हें संख्या कहते हैं।

अंकगणित में कुल 10 संख्याएँ (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) होती हैं। जिनकी मदद से बड़ी-बड़ी संख्याएँ बनती हैं। शून्य को पूर्ण संख्या माना गया हैं शून्य जिस संख्या के पीछे लग जाता हैं उस संख्या का मान 10 गुना बढ़ जाता हैं।

जैसे :-

• 2 के पीछे 0 लगाने से 20 (बीस) हो जाता हैं।
• 5 के पीछे 0 लगाने से 50 (पचास) हो जाता हैं।
• 10 के पीछे 00 लगाने से 1000 (एक हजार) हो जाता हैं।
• 20 के पीछे 000 लगाने से 20,000 (बीस हजार) हो जाता हैं।
• 500 के पीछे 0000 लगाने से 50,00000 (पचास लाख) हो जाता हैं।

संख्या को अंग्रेजी में Number कहाँ जाता हैं।

संख्या प्रणाली किसे कहते हैं

0, 1, 2, 3, 4, 5, 6, 7, 8 एवं 9 को अंक कहते हैं। अंकों से मिलकर संख्याएँ बनती हैं। संख्या को लिखने का तरीका संख्या पद्धति या संख्या प्रणाली कहलाता हैं।

किसी संख्या को लिखने के लिए दो तरह की प्रणाली प्रचलित हैं।

• दाशमिक प्रणाली
• अंतराष्ट्रीय प्रणाली

1. दाशमिक प्रणाली (Decimal System)

दाशमिक प्रणाली को भारतीय अरबी प्रणाली के नाम से भी जाना जाता हैं।

नीचे बनी तालिका देख कर आप स्पष्ट रूप से समझ सकते हैं इसमें दाईं से बाई ओर क्रमशः इकाई, दहाई सैकड़ा, हजार, दस हजार, लाख, दस लाख, करोड़, दस करोड़, अरब, दस अरब आदि लिखकर संख्याओं को उसके नीचे उचित स्थान पर लिखते हैं।

जैसे:- अस्सी अरब, बत्तीस करोड़, पाँच लाख, छः हजार, नौ सौ चौबीस।

स्थानीय मान को तालिका बनाकर लिखने पर

दस अरब	अरब	दस करोड़	करोड़	दस लाख	लाख	दस हजार	हजार	सैकड़ा	दहाई	इकाई
8	0	3	2	0	5	0	6	9	2	4

संख्या अंकों में = 80,32,05,06,924

2. अंतराष्ट्रीय प्रणाली (International System)

अंतराष्ट्रीय प्रणाली में आप नीचे बनी हुई तालिका को स्पष्ट देखकर समझ सकते हैं इसमें दाईं से बाईं और क्रमशः इकाई, दहाई, सैकड़ा, हजार, दस हजार, सौ हजार, मिलियन, दस मिलियन, सौ मिलियन, बिलियन, दस बिलियन, सौ बिलियन आदि।

जैसे :- पचास बिलियन, सात सौ नब्बे मिलियन, आठ सौ पाँच हजार, चार सौ चौअन

अंतरराष्ट्रीय प्रणाली को तालिका बनाकर लिखने पर

सौ बिलियन	दस बिलियन	बिलियन	सौ मिलियन	दस मिलियन	मिलियम	सौ हजार	दस हजार	हजार	सैकड़ा	दहाई	इकाई
0	5	0	7	9	0	8	0	5	4	5	4

संख्या अंकों में, = 50, 790, 805, 454

किसी संख्या में अंकों का जातीय मान

कोई भी संख्या जो दो या दो से अधिक अंकों से मिलकर बनी होती हैं उसमें अंक का अपना ही मान होता हैं।

जातीय मान (Face Value) :- किसी अंक का जातीय मान किसी संख्या में उसके स्थान पर निर्भर नहीं करता हैं उस अंक का जो वास्तविक मान होता हैं उसे ही जातीय मान कहते हैं।

जैसे :- 5,42,73,679 में 7 का जातीय मान 7 ही हैं चाहे वह दहाई के स्थाना वाला 7 हो या दस हजार के स्थान वाला 7 हो।

किसी संख्या में अंकों का स्थानीय मान

स्थानीय मान (Place Value) :- किसी अंक का स्थानीय मान किसी संख्या में उसके स्थान पर निर्भर करता हैं।

जैसे:- 56783 में 8 का स्थानीय मान = 8 × 10 = 80

नोट :- शून्य (0) का जातीय मान एवं स्थानीय मान हमेशा 0 होता हैं।

अधिक जानकारी के लिए स्थानीय मान और जातीय मान की पोस्ट पढ़िए।

संख्याओं के प्रकार

संख्याएँ 12 प्रकार की होती हैं।

1. प्राकृतिक संख्याएँ → 1, 2, 3, 4, 5, ………
2. सम संख्याएँ → 2, 4, 6, 8, 10, ………
3. विषम संख्याएँ → 1, 3, 5, 7, 9, ………
4. पूर्णांक संख्याएँ → -3, -2, -1, 0, 1, 2, 3, ………
5. पूर्ण संख्याएँ → 0, 1, 2, 3, 4, ………
6. भाज्य संख्याएँ → 4, 6, 8, 9, ………
7. अभाज्य संख्याएँ → 2, 3, 5, 7, 11, ………
8. सह अभाज्य संख्याएँ → (5, 7) , (2, 3)
9. परिमेय संख्याएँ → √4, 7/5, 2/3, 3
10. अपरिमेय संख्याएँ → √5, √7, √11, √13
11. वास्तविक संख्याएँ→ √4, √11, 4/7
12. अवास्तविक संख्याएँ → √-6, √-5, √-29

नीचे हम संख्याओं के 12 प्रकारों को विस्तार से पड़ेगें एवं समझेगें।

1. प्राकृतिक संख्याएँ (Natural Number)

गिनती में उपयोग की जाने वाली सभी संख्याएँ प्राकृतिक संख्याएँ कहलाती हैं। प्राकृतिक संख्याओं में 0 को शामिल नहीं किया जाता। प्राकृतिक संख्याएँ 1 से शुरू होकर अनंत तक जाती हैं।

जैसे :- 1, 2, 3, 4, 5, 6, 7, 8, 9……………अनंत

2. सम संख्याएँ (Even Number)

ऐसी प्राकृतिक संख्याएँ जो 2 से पूर्णतः विभाजित होती हैं उन्हें सम संख्याएँ कहा जाता हैं।

जैसे :- 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…….………अनंत

3. विषम संख्याएँ (Odd Number)

ऐसी प्राकृतिक संख्याएँ जो 2 से पूर्णतः से विभाजित न हो उन्हें विषम संख्याएँ कहते हैं।

जैसे :- 1, 3, 5, 7, 9, 11, ……………अनंत

4. पूर्णांक संख्याएँ (Integer Number)

धनात्मक, ऋणात्मक और जीरों से मिलकर बनी हुई संख्याएँ पूर्णांक संख्याएँ होती हैं।

जैसे :- -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5……………..………अनंत

पूर्णांक संख्याएँ तीन प्रकार की होती हैं।

• धनात्मक संख्याएँ
• ऋणात्मक संख्याएँ
• उदासीन पूर्णांक

(a). धनात्मक संख्याएँ :- एक से लेकर अनंत तक की सभी धनात्मक संख्याएँ धनात्मक पूर्णांक हैं।

(b). ऋणात्मक संख्याएँ :- 1 से लेकर अनंत तक कि सभी ऋणात्मक संख्याएँ त्रणात्मक पूर्णांक हैं।

(c). उदासीन पूर्णांक :- ऐसा पूर्णांक जिस पर धनात्मक और ऋणात्मक चिन्ह का कोई प्रवाह ना पढ़े और यह जीरो होता हैं।

5. पूर्ण संख्याएँ (Whole Number)

प्राकृतिक संख्याएँ में जीरो को शामिल कर लेने पर यह पूर्ण संख्याएँ बनती हैं। पूर्ण संख्याएँ 0 से शुरू होकर अनंत तक जाती हैं।

जैसे :- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9……….………अनंत

6. भाज्य संख्याएँ (Composite Number)

ऐसी प्राकृत संख्याएँ जो स्वंय और 1 से विभाजित होने के अतिरिक्त कम से कम किसी एक अन्य संख्याओं से विभाजित हो उन्हें भाज्य संख्याएँ कहते हैं।

जैसे :- 4, 6, 8, 9, 10, 12, 14, 16, 18, 20……..………अनंत

7. अभाज्य संख्याएँ (Prime Number)

ऐसी प्राकृतिक संख्याएँ जो सिर्फ स्वंय से और 1 से विभाजित हो और किसी भी अन्य संख्या से विभाजित न हो उन्हें अभाज्य संख्याएँ कहते हैं।

जैसे :- 2, 3, 5, 11, 13, 17, ………

8. सह अभाज्य संख्या (Co-prime Number)

कम से कम 2 अभाज्य संख्याओ का ऐसा समूह जिसका (HCF) 1 हो सह अभाज्य संख्याएँ कहलाती हैं।

जैसे :- (5, 7) , (2, 3)

9. परिमेय संख्याएँ (Rational Number)

ऐसी सभी संख्याएँ जिन्हें p/q के रूप में लिखा जा सकता हैं। उन्हें परिमेय संख्याएँ कहते है।

(q हर का मान जीरो नहीं होना चाहिए)

जैसे :- 5, 2/3, 11/4, √25

10. अपरिमेय संख्याएँ (Irrational Number)

ऐसी संख्याएँ जिन्हें p/q के रूप में नही लिखा जा सकता और मुख्यतः उन्हें (√) के अंदर लिखा जाता हैं। और कभी भी उनका पूर्ण वर्गमूल नहीं निकलता अपरिमेय संख्याएँ कहते हैं।

जैसे :- √3, √7, √11, √17, √117, √223

नोट:- (π एक अपरिमेय संख्याएँ हैं।)

11. वास्तविक संख्या (Real Number)

परिमेय और अपरिमेय संख्याओ को सम्मलित रूप से लिखने पर वास्तविक संख्या प्राप्त होती हैं।

जैसे :- 2/5, 4/7, 11/13, √5, √11, √47,

12. अवास्तविक संख्या (Unreal Number)

यह एक काल्पनिक संख्या है जिसका वास्तविक नहीं होता हैं अवास्तविक संख्या या काल्पनिक संख्या को इकाई से दर्शाया जाता हैं।

जैसे :- √- 2, √-4, √-12, √-17, √-107 आदि।

महत्वपूर्ण बिंदु :-

1. 1 न तो भाज्य संख्या हैं न ही अभाज्य संख्या हैं।
2. 2 सबसे छोटी अभाज्य संख्या हैं।
3. 2 एक ऐसी संख्या हैं जो अभाज्य भी हैं तथा सम भी हैं।
4. सभी अभाज्य संख्याएं विषम हैं।
5. 1 से 25 तक 9 अभाज्य संख्याएं हैं।
6. 1 से 50 तक 15 अभाज्य संख्याएं हैं।
7. 50 से 100 तक 10 अभाज्य संख्याएं हैं।
8. 1 से 100 तक 25 अभाज्य संख्याएं हैं।
9. किन्हीं भी दो या दो से अधिक सम संख्याओं को जोड़ने पर सदैव सम संख्या प्राप्त होती हैं।
10. यदि एक सम संख्या में एक विषम संख्या जोड़ी जाए तो सदैव एक विषम संख्या प्राप्त होगी।
11. यदि दो विषम संख्याओं को आपस में जोड़ा जाता है तो सदैव एक सम संख्या प्राप्त होगी।
12. किसी भी सम संख्या की जितनी भी घात की जाए परिणाम सदैव सम संख्या होगा।
13. किसी भी विषम संख्या की जितनी भी घात की जाए परिणाम सदैव विषम संख्या होगा।

बड़ी-से-बड़ी एवं छोटी-से-छोटी संख्याएं

• एक अंक की सबसे छोटी संख्या 1 हैं।
• एक अंक की सबसे बड़ी संख्या 9 हैं।
• दो अंको की सबसे छोटी संख्या 10 हैं।
• दो अंको की सबसे बड़ी संख्या 99 हैं।
• तीन अंको की सबसे छोटी संख्या 100 हैं।
• तीन अंको की सबसे बड़ी संख्या 999 हैं।
• चार अंको की सबसे छोटी संख्या 1000 हैं।
• चार अंको की सबसे बड़ी संख्या 9999 हैं।
• पाँच अंको की सबसे छोटी संख्या 10000 हैं।
• पाँच अंको की सबसे बड़ी संख्या 99999 हैं।

संख्याओं पर आधारित प्रश्न और उत्तर

Q.1 संख्या 987653 में 7 का स्थानीय मान क्या हैं?
A. 8
B. 8926
C. 7000
D. 8000

हल:- प्रश्नानुसार,
संख्या 987653 में 7 का स्थानीय मान = 7 × 1000
स्थानीय मान = 7000
Ans. 7000

Q.2 0.06537 में 5 का स्थानीय मान क्या हैं?
A. 5
B. 5/100
C. 5/1000
D. 65/1000

हल:- प्रश्नानुसार,
0.06537 में 5 का स्थानीय मान
स्थानीय मान = 0.005
स्थानीय मान = 5/1000
Ans. 5/1000

Q.3 678954 में प्रत्येक संख्या का स्थानीय मान बताइए?

हल:- 678954 में,
4 का स्थानीय मान = 4 × 1 = 4 हैं।
5 का स्थानीय मान = 5 × 10 = 50 हैं।
9 का स्थानीय मान = 9 × 100 = 900 हैं।
8 का स्थानीय मान = 8 × 1000 = 8000 हैं।
7 का स्थानीय मान = 7 × 10000 = 70000 हैं।
6 का स्थानीय मान = 6 × 100000 = 600000 हैं।

Q.4 45678 में 5 का जातीय मान क्या हैं?

हल:- प्रश्नानुसार,
संख्या 45678 में 5 का जातीय मान = 5
Ans. 5

Q.5 67543 में प्रत्येक संख्या का जातीय मान बताइए?

हल:- 67543 में,
6 का जातीय मान = 6
7 का जातीय मान = 7
5 का जातीय मान = 5
4 का जातीय मान = 4
3 का जातीय मान = 3

Q.6 7682463 में 6 के स्थानीय मूल्यों में क्या अंतर हैं?
A. 699940
B. 599940
C. 682933
D. 599993

हल:- प्रश्नानुसार,
7682463 का स्थानीय मान एवं जातीय मान
6 का स्थानीय मान = 600000
6 का जातीय मान = 60
6 के स्थानीय मूल्यों में अंतर = 600000 – 60
अंतर = 599940
Ans. 599940

Q.7 7765 को किसी संख्या से भाग देने पर भागफल 45 तथा शेष 25 आता हैं भाजक क्या हैं?
A. 165
B. 172
C. 175
D. 180

हल:- प्रश्नानुसार,
सूत्र :- भाजक = (भाज्य – शेषफल)/भागफल
भाजक = (7765 – 25)/45
भाजक = 172
Ans. 172

Q.8 43 × 44 × 45 ……… × 48 में इकाई का अंक क्या होगा?
A. 3
B. 1
C. 2
D. 0

हल:- प्रश्नानुसार,
43 × 44 × 45 × 47 × 48 में इकाई के अंकों का
गुणनफल = 3 × 4 × 5 × 6 × 7 × 8 = 20160
इकाई उपस्थित अभीष्ट अंक = 0
Ans. 0

Q.9 गुणन (2467)¹⁵³ × (341)⁷² × (225)⁷²¹ में इकाई का अंक हैं?
A. 1
B. 3
C. 5
D. 7

हल:- प्रश्ननानुसार,
(2467)¹⁵³ × (341)⁷² × (225)⁷²¹
(2467)¹⁵³ में इकाई का अंक
(2467)¹⁵³⁄₄ का शेष में इकाई का अंक
(7)¹ में इकाई का अंक = 7
(341)⁷² में इकाई का अंक = 1
(225)⁷²¹ में इकाई का अंक = 5
अतः अभीष्ट इकाई का अंक = 7 × 1 × 5
अभीष्ट इकाई का अंक = 35
इकाई का अंक = 5
अतः इकाई का अंक 5 होगा।
Ans. 5

Q.10 संख्या 17¹⁹⁹⁹ + 11¹⁹⁹⁹ − 7¹⁹⁹⁹ के इकाई के स्थान में अंक हैं?
A. 1
B. 3
C. 5
D. 7

हल:- प्रश्ननानुसार,
17¹⁹⁹⁹ + 11¹⁹⁹⁹ − 7¹⁹⁹⁹
17¹⁹⁹⁹ में इकाई का अंक
(17)¹⁹⁹⁹⁄₄ का शेष में इकाई का अंक
(7)³ में इकाई का अंक = 3
(11)¹⁹⁹⁹ में इकाई का अंक = 1
(7)¹⁹⁹⁹ में इकाई का अंक = 3
अतः अभीष्ट इकाई का अंक = 3 + 1 − 3
इकाई का अंक = 4 − 3
इकाई का अंक = 1
अतः इकाई का अंक 1 होगा।
Ans. 5

Q.11 [(251)⁹⁸ + (21)²⁹ − (106)¹⁰⁰ + (705)³⁵ − 16⁴ + 259] के सरलीकृत रूप में इकाई का अंक बताइए?

इस प्रकार की स्थिति में आधार वाली संख्या में क्रमशः 0, 1, 5, 6, इकाई अंक होने पर उत्तर भी क्रमशः 0, 1, 5, और 6 ही होगा।

[(251)⁹⁸ + (21)²⁹ − (106)¹⁰⁰ + (705)³⁵ − 16⁴ + 259]
1 + 1 − 6 + 5 − 6 + 9
16 – 12
4
Ans. 4

Q.12 यदि किसी संख्या का वर्ग किया जाए, तो इकाई के स्थान पर कौन सा अंक होगा?
A. 7
B. 3
C. 8
D. 5

हल:- प्रश्नानुसार,
यदि किसी संख्या का वर्ग किया जाए, तो इकाई के स्थान पर
0, 1, 4, 5, 6 और 9 हो सकता हैं।
Ans. 5

Q.13 1/4 तथा 1/3 के मध्य एक परिमेय संख्या हैं?
A. 7/24
B. 7/12
C. 1/12
D. 2/15

हल:- प्रश्नानुसार,
1/2 (1/4 + 1/3)
1/2 × (3 + 4)/12
1/2 × 7/12
7/24
Ans. 7/24

Q.14 50 और 100 के बीच अभाज्य संख्याओं की संख्या हैं?
A. 8
B. 9
C. 11
D. 10

हल:- प्रश्नानुसार,
50 और 100 के बीच अभाज्य संख्या
53, 59, 61, 71, 73, 79, 83, 89 और 97 हैं।
कुल संख्या = 9
Ans. 9

Q.15 42² – 38² = 4k दिया हो, तो K का मान होगा?
A. 4
B. 16
C. 80
D. 96

हल:- प्रश्नानुसार,
4k = 42² – 38²
4k = (42 + 38) (42 – 38)
4k = 80 × 4
k = (80 × 4)/4
k = 80
Ans. 80

Q.16 अगर (a + b)/c = (b + c)/a = (c + a)/b = k हो, तो k का मान क्या हैं?
A. 0
B. 1
C. 2
D. a + b + c

हल:- प्रश्नानुसार,
(a + b)/c = (b + c)/a = (c + a)/b = k
a + b = kc
b + c = ka तथा
a + c = kb
2 (a + b + c) = k (a + b + c)
K = 2
Ans. 2

Q.17 यदि a/3 = b/4 = c/7 हो, तो (a + b + c)/c का मान हैं?
A. √2
B. 2
C. 7
D. 1/√7

हल:- माना,
a/3 = b/4 = c/7 = k
a = 3k, b = 4k, c = 7k
(a + b + c)/c
(3k + 4k + 7k)/7k
14k/7k
2
Ans. 2

Q.18 यदि a = 0.25, b = 0.05, c = 0.5 हो तो (a² – b² – c² – 2bc)/a² + b² − 2ab − c² का मान होगा?
A. ⁷⁄₈
B. ¹⁴⁄₁₇
C. 7
D. ²⁵⁄₁₆

हल:- प्रश्नानुसार,
a = 0.25,
b = 0.05,
c = 0.5
(a² – b² – c² – 2bc)/a² + b² − 2ab − c²
a² – (b + c)²/(a – b)² − c²
(a – b – c)(a + b + c)/(a – b – c)(a + b + c)
(0.25 – 0.05 + 0.5)/(0.25 + 0.05 + 0.5)
0.78/0.80
7/8
Ans. ⁷⁄₈

Q.19 यदि (2a + b)/(a + 4b) = 3 हैं, तो (a + b)/(a + 2b) का मान हैं?
A. 5/9
B. 2/7
C. 10/9
D. 10/7

हल:- प्रश्नानुसार,
(2a + b)/(a + 4b) = 3
2a + b = 3a + 12b
a/b = -11
(a + b)/(a + 2b) = (a/b + 1)/(a/b + 2)
= (-11 + 1)/(-11 + 2)
= -10/-9
= 10/9
Ans. 10/9

Q.20 यदि (x + 1) का व्युत्क्रम (x – 1) हैं तो x का मान हैं (x ≠ 1) –
A. √2
B. 3
C. 1√3
D. x + 2

हल:- प्रश्नानुसार,
x + 1 = 1/x – 1
x² – 1 = 1
x² = 1 + 1
x² = 2
x = √2
Ans. √2

Q.21 संख्या 5k3457 में k का मान क्या होगा जबकि संख्या 11 से पूर्णतया हो जाए?
A. 1
B. 2
C. 4
D. 3

हल:- प्रश्नानुसार,
5 + 3 + 5 = k + 4 + 7
13 = k + 11
k = 13 – 11
k = 2
वह संख्या 11 से पूर्णतया विभाजित होती हैं जिसके सम स्थान के अंको का योग विषम स्थान के अंकों के योग के बराबर या उनका अंतर 11 से विभाजित हो।
Ans. 2

Q.22 100 और 1000 के बीच की किसी संख्या में से उसके अंकों का योगफल घटा देने से प्राप्त संख्या सदैव विभाजित होंगी?
A. 3 से
B. 6 से
C. 5 से
D. 12 से

हल:- प्रश्नानुसार,
100 और 1000 के बीच संख्या
= 100x + 10y + z
[जहाँ 0 ≤ x, y, z ≤ 9]
(100x + 10y + z) – (x + y + z)
= 99x + 9y
= 9 (11x + y)
= 9 का गुणज
अतः संख्या 9 का गुणज हैं जोकि 3 का भी गुणज होगा।
Ans. 3

Q.23 यदि x और y किसी संख्या 653 xy का दो अंक हो और वह संख्या 80 से भाज्य हो, तो (x + y) का मान क्या होगा?
A. 2
B. 3
C. 4
D. 6

हल:- प्रश्नानुसार,
चूंकि संख्या 653 xy, 80 से भाज्य हैं।
अतः यह संख्या 8 और 10 दोनों से भाज्य होगी।
653 xy को 10 से भाज्य होने के लिए y के स्थान पर शून्य होना चाहिए।
और 8 से भाज्य होने के लिए शेष अंतिम तीन अंक 8 से भाज्य होना चाहिए।
अतः संख्या 65360 होगी
जहाँ x = 6 और y = 0
x + y = 6 + 0
= 6
Ans. 6

Q.24 200 और 600 के बीच कितनी संख्याएँ हैं जो 4, 5 और 6 से पूर्णतः भाज्य हैं?
A. 5
B. 8
C. 6
D. 9

हल:- प्रश्नानुसार,
4, 5 और 6 का ल. संख्या = 60
200 से अधिक वह छोटी संख्या जो 60 से विभाज्य हो – 240
200 तथा 600 के बीच बड़ी से बड़ी संख्या जो 60 से विभाज्य हो = 540
माना,
अभीष्ट संख्या = n
540 = 240 + (n – 1) 60
540 = 240 + (n – 1) 60
(n – 1) = (540 – 240)/60
(n – 1) = 300/60
(n – 1) = 5
n = 5 + 1
n = 6
Ans. 6

Q.25 किन्हीं तीन सतत प्राकृत संख्याओं के गुणनफल को पूरा – पूरा विभाजित करने वाली बड़ी से बड़ी संख्या हैं?
A. 8
B. 6
C. 12
D. 16

हल:- प्रश्नानुसार,
तीन क्रमागत प्राकृत संख्या = 1, 2, 3
1 × 2 × 3 = 6
अर्थात वैसी सभी संख्या 6 से विभाजित होंगे।
Ans. 6

Q.26 यदि (x + 1) : 8 = 3.75 : 7, हो तो x का मान हैं?
A. 25/9
B. 23/7
C. 18/4
D. 19/5

हल:- प्रश्नानुसार,
(x + 1)/8 = 3.75/7
7(x + 1) = 3.75 × 8
(x + 1) = (3.75 × 8)/7
(x + 1) = 30/7
x = 30/7 – 1
x = (30 – 7)/7
x = 23/7
Ans. 23/7

Q.27 यदि a : (b + c) = 1 : 3 और c : (a + b) = 5 : 7 हो, तो b : (c + a) बराबर होगा?
A. 1/2
B. 2/3
C. 5/2
D. 2/1

हल:- प्रश्नानुसार,
a : (b + c) = 1 : 3
a/(b + c) = 1/3 या a = (b + c)/3
तथा c : (a + b) = 5 : 7
c/a + b = 5/7
7c = 5a + 5b
7c = 5 × b + c/3 + 5b
21c = 5b + 5c + 15b
c = 20b/16
c = 5b/4
b/(c + a) = b/(5b/4 + 3b)/4
b/(c + a) = b/(5b + 3b)/4
b/(c + a) = b/(8b/4)
b/(c + a) = b/2b
b/(c + a) = 1/2
Ans. 1/2

Q.28 9 | 3 − 5 |-5 | 4 | ÷ 10 / -3(5) −2 × 4 ÷ 2 मान ज्ञात कीजिए?
A. ⁹⁄₁₀
B. ⁻⁸⁄₂₇
C. ⁻¹⁶⁄₁₉
D. ⁴⁄₇

हल:- प्रश्नानुसार,
9 | 3 − 5 |-5 | 4 | ÷ 10 / -3(5) −2 × 4 ÷ 2
9 × 2 × -5 × 4 × ÷ 10 / -3 × (5) −2 × 2
18 × -5 × 4/10 / -15 – 4
16/-19
Ans. ⁻¹⁶⁄₁₉

Q.29 3.75 × 10⁻⁷, 3³⁄₄ × 10⁻⁷, 375 × 10⁻⁹ तथा ³⁄₈ × 10⁻⁷ दी गई हैं इनमें से कौन सी 0.000000375 के तुल्य नहीं हैं?
A. 3.75 × 10⁻⁷
B. 375 × 10⁻⁷
C. 3³⁄₈ × 11⁻⁹
D. ³⁄₈ × 10⁻⁷

हल:- प्रश्नानुसार,
3.75 × 10⁻⁷, 3³⁄₄ × 10⁻⁷, 375 × 10⁻⁹
3³⁄₄ × 10⁻⁷ = 3.75 × 10⁻⁷
3³⁄₄ × 10⁻⁷ = 0.000000375
3.75 × 10⁻⁹ = 0.000000375
³⁄₈ × 10⁻⁷ = 0.375 × 10⁻⁷
³⁄₈ × 10⁻⁷ = 0.000000375
∴ ³⁄₈ × 10⁻⁷
0.000000375 के तुल्य नहीं हैं।

Q.30 यदि x/y हो तो x² + y²/x² ⁻ y² का मान होगा?
A. ³⁶⁄₂₅
B. ²⁵⁄₃₆
C. ⁶¹⁄₁₁
D. ¹¹⁄⁶¹

हल:- प्रश्नानुसार,
x² + y²/x² ⁻ y²
(x/y)² + 1/(x/y)² – 1
(x/y)² + 1/(x/y)² – 1 [y² से भाग देने पर]
(6/5)² + 1/(6/5)² – 1
(36/25 + 1)/(36/25 – 1)
(36 + 25)/25 / (36 – 25)/25
61/25 / 11/25
61/25 × 25/11
61/11
Ans. ⁶¹⁄₁₁

FAQ

जरूर पढ़िए :

• वर्गमूल
• घनमूल
• सांख्यिकी योग्यता

उम्मीद हैं आपको संख्या की पोस्ट पसंद आयीं होगीं यदि आपको संख्याओं की जानकारी पसंद आयीं हो तो अपने दोस्तों के साथ जरूर शेयर करें धन्यवाद।