इस पेज पर आप पूर्णांक संख्या की जानकारी पढ़ने वाले हैं तो आर्टिकल को पूरा जरूर पढ़िए।
पिछले पेज पर हमने सम संख्या और विषम संख्या की जानकारी शेयर की हैं तो पोस्ट को जरूर पढ़िए।
चलिए इस पेज पर पूर्णांक संख्याएँ किसे कहते हैं इसके उदाहरण को हल सहित पढ़ते और समझते हैं।
Table of Contents
पूर्णांक संख्या किसे कहते हैं
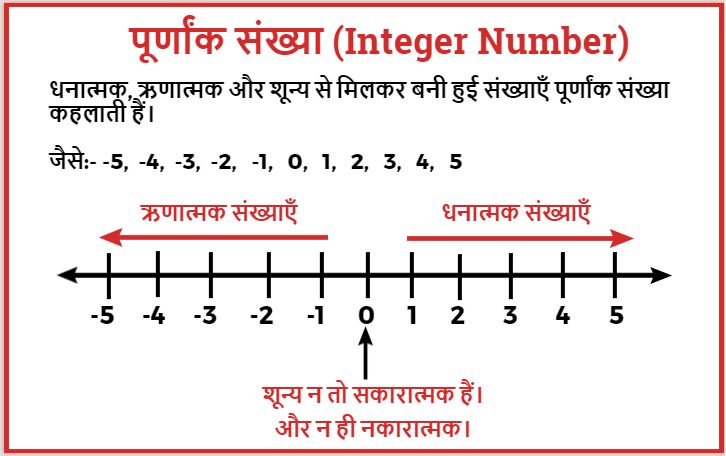
धनात्मक, ऋणात्मक और शून्य से मिलकर बनी हुई संख्याएँ पूर्णांक संख्या कहलाती हैं।
जैसे:- -5,-4, -3, -2, -1, 0, 1, 2, 3, 4, 5
पूर्णांक संख्या को अंग्रेजी में Integer Number कहते हैं।
पूर्णांक संख्या के प्रकार
पूर्णांक संख्याएँ तीन प्रकार की होती हैं।
- धनात्मक संख्याएँ
- ऋणात्मक संख्याएँ
- उदासीन पूर्णांक
1. धनात्मक पूर्णांक
एक से लेकर अनंत तक की सभी धनात्मक संख्याएँ धनात्मक पूर्णांक कहलाती हैं।
कोई भी पूर्णांक संख्या जिसके आगे धनात्मक या ऋणात्मक का कोई चिन्ह नहीं लगा हो ऐसी संख्याएँ धनात्मक पूर्णांक कहलाती हैं।
जैसे :- 1, 2, 3, 4, 5, 6, 7, 8, 9, …………. ∞
ये सभी संख्याएँ धनात्मक पूर्णांक के अंतर्गत आती हैं।
धनात्मक संख्याएँ पूर्णांक संख्या रेखा पर शून्य के दायीं और स्थित होती हैं अतः ये संख्याएँ धनात्मक पूर्णांक के अंतर्गत आएगी।
2. ऋणात्मक पूर्णांक
1 से लेकर अनंत तक कि सभी ऋणात्मक संख्याएँ ऋणात्मक पूर्णांक कहलाती हैं।
ऋणात्मक पूर्णांक संख्याओं के आगे ऋणात्मक चिन्ह लगा होता है। ऋणात्मक संख्याएँ संख्या रेखा पर शून्य के बायीं और स्थित होती हैं। जो संख्याएँ शून्य से छोटी होती है वे ऋणात्मक पूर्णांक कहलाती हैं।
जैसे :- -1, -2, -3, -4, -5, -6, -7, -8, -9 ……..……∞
ये सभी संख्याएँ ऋणात्मक पूर्णांक के अंतर्गत आती हैं।
3. उदासीन पूर्णांक
ऐसा पूर्णांक जो न तो कोई धनात्मक पूर्णांक है और न ही ऋणात्मक पूर्णांक है। उदासीन पूर्णांक कहलाता हैं। यह शून्य पूर्णांकों के अंतर्गत आता हैं।
जैसे :- 3, -2, -1, 0, 1, 2, 3, ………………∞
पूर्णांक संख्या के गुण
पूर्णांक संख्या के गुण दो प्रकार के होते हैं।
- पूर्णांक संख्या के घटाव के गुण
- पूर्णांक संख्या के गुणा
1. पूर्णांक संख्या के घटाव के गुण
पूर्णांक संख्या के घटाव के गुण पाँच प्रकार के होते हैं।
(a). योग के अंतगर्त संवृत –
पूर्णांक संख्या योग के अंतगर्त संवृत नियम का पालन करती है।
अर्थात इस नियम के अनुसार किन्ही दो पूर्णांकों को जोड़ने पर प्राप्त परिणाम एक पूर्णांक ही प्राप्त होता है।
जैसे:-
2 + 2 = 4
5 + 5 = 10
10 + 10 = 20
50 + 50 = 100
यहाँ पर 4, 10, 20 एवं 50 एक पूर्णांक संख्या है।
b). व्यवकलन / घटाव के अंतर्गत संवृत
पूर्णांक संख्याए घटाव के अंतगर्त संवृत नियम का पालन करती है। इसके अनुसार जब किन्ही दो पूर्णांकों को आपस में घटाया जाता है तो प्राप्त परिणाम भी एक पूर्णांक संख्या प्राप्त होगी।
जैसे:-
8 – 4 = 4
24 – 12 = 12
50 – 24 = 26
100 – 86 = 14
यहाँ पर 4, 12, 26 एवं 14 एक पूर्णांक संख्या है।
c). क्रमविनिमेय गुण
पूर्णांक संख्याओ को जोड़ने पर यह क्रमविनिमेय नियम का पालन करती है। अर्थात दो पूर्णांकों को किसी भी क्रम में जोड़ने पर परिणाम समान रहता है।
जैसे:-
5 + 3 = 8
3 + 5 = 8
दोनों परिणाम समान है इसलिए यह क्रमविनिमेय नियम का पालन करते हैं।
d). साहचर्य गुण
पूर्णांकों को जोड़ने एवं घटाने में साहचर्य गुण का पालन करते है।
a + (b + c) = (a + b) + c
e). योज्य तत्समक
पूर्ण संख्याओं के लिए शून्य एक योज्य तत्समक है।
a + 0 = a = 0 + a
2. पूर्णांक संख्या के गुणा
सबसे पहले गणितज्ञ जिन्होंने 1770 ईस्वी में अपनी पुस्तक “Ankitung zur Algebra” में यह सिद्ध करने का प्रयास किया कि (–1) × (–1) = 1 होता है।
जैसे:-
(-2) × (-2) = 4
(-5) × (-7) = 35
(-5) × (-8) = 40
(-9) × (-5) = 45
a). गुणन के अंतर्गत संवृत
पूर्णांक गुणन के अंतगर्त संवृत होते है। सभी पूर्णांकों a तथा b के लिए a × b एक पूर्णांक होता है ।
जैसे:-
2 × 5 = 10
4 × 6 = 24
6 × 7 = 42
8 × 8 = 64
b). गुणन की क्रमविनिमेयता
पूर्णांक संख्याए गुणन के प्रति क्रमविनिमेयता दर्शाती है। व्यापक रूप में, किन्हीं दो पूर्णांकों a तथा b के लिए गुणन की क्रम विनिमेयता
a × b = b × a
जैसे:-
4 × 5 = 20
5 × 4 = 20
c). शून्य से गुणन
पूर्णांक संख्या जब किसी को शून्य से गुणा किया जाता है तो गुणनफल के रूप में शून्य प्राप्त होता है।
a × 0 = 0 × a = 0
जैसे:-
2 × 0 = 0
7 × 0 = 0
d). गुणनात्मक तत्समक
पूर्ण संख्याओं के लिए 1 गुणनात्मक तत्समक है।
a × 1 = 1 × a = a
e). गुणन साहचर्य गुण
यह गुणन साहचर्य गुण का पालन करती है।
(a × b) × c = a × (b × c)
पूर्णांक संख्या के महत्वपूर्ण बिन्दु
- संख्या 0, 1, -1, 2, -2, 3, -3, ……….…….∞ पूर्णांक संख्या कहलाती हैं।
- संख्या +1, +2, +3, +4, ……………∞ धनात्मक पूर्णांक कहलाती हैं।
- संख्या -1, -2, – 3, – 4, ……………….∞ पूर्णांक कहलाती हैं।
- संख्या 0, + 1, + 2, + 3, + 4, ऋणेत्तर पूर्णांक कहलाते हैं।
- ऋणेत्तर पूर्णांक पूर्ण संख्या ही कहलाती हैं।
सभी धनात्मक पूर्णांक संख्या रेखा पर 0 के दायीं ओर तथा सभी ऋणात्मक पूर्णांक संख्या रेखा पर 0 के बायीं ओर स्थित होते हैं।
दो पूर्णांक जिनका योग शून्य हो एक-दूसरे के योज्य प्रतिलोम कहलाते हैं। ये एक दूसरे के ऋणात्मक भी कहलाते हैं।
पूर्णांकों का जोड़, घटाना, गुना एवं भाग
दो पूर्णांकों के योग का नियम
(-) + (-) = (+)
(+) + (+) = (+)
(-) + (+) = (-)
(+) + (-) = (-)
समान चिन्ह वाले पूर्णांक का जोड़
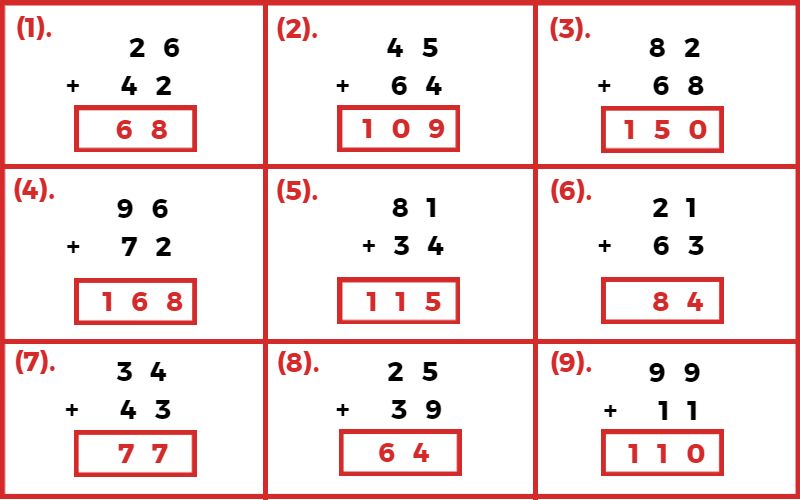
विभिन्न चिन्ह वाले पूर्णांकों का जोड़

दो पूर्णांकों को घटाने के नियम
- (-) – (-) = (-)
- (+) – (+) = (-)
- (-) – (+) = (+)
- (+) – (-) = (+)
समान चिन्ह वाले पूर्णांकों को घटाना
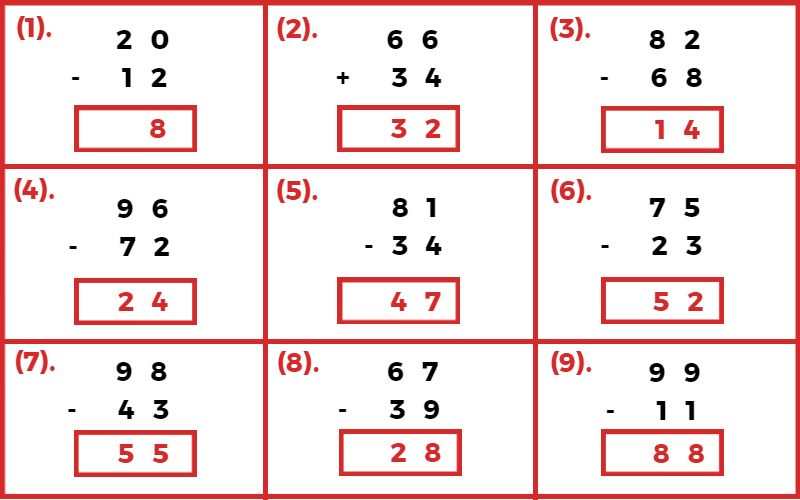
विभिन्न चिन्ह वाले पूर्णांकों को घटाना

दो पूर्णांकों के गुणनफल का नियम
- (-) × (-) = (+)
- (+) × (+) = (+)
- (-) × (+) = (-)
- (+) × (-) = (-)
समान चिन्ह वाले पूर्णांकों का गुणनफल
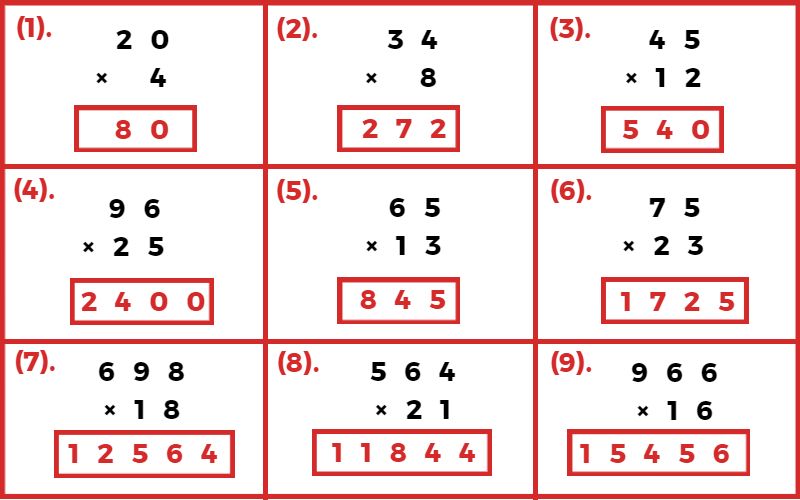
विभिन्न चिन्ह वाले पूर्णांकों का गुणनफल

दो पूर्णांकों के विभाजन के नियम
- (-) ÷ (-) = (+)
- (+) ÷ (+) = (+)
- (-) ÷ (+) = (-)
- (+) ÷ (-) = (-)
समान चिन्ह वाले पूर्णांकों को विभाजन
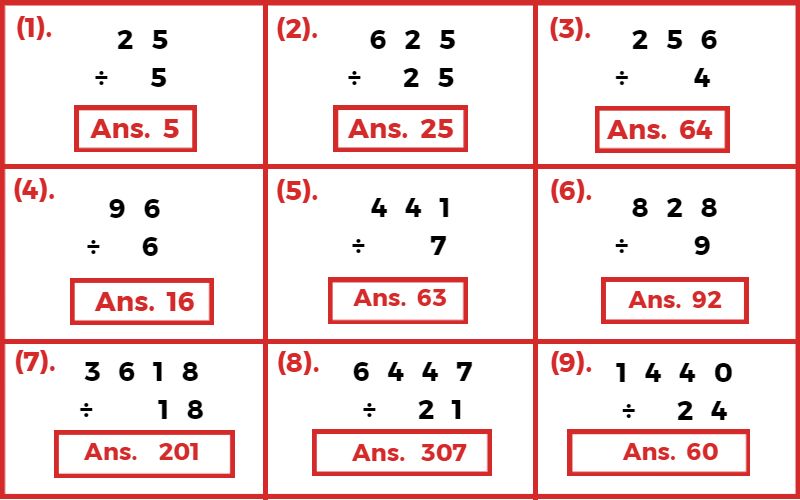
विभिन्न चिन्ह वाले पूर्णांकों को विभाजन

पूर्णांक संख्या से संबंधित प्रश्न उत्तर
Q.1 (-8), (-4) पूर्णांकों के युग्मों के योग ज्ञात कीजिए?
(A). 12
(B). -12
(C). 8
(D). -4
हल:- प्रश्नानुसार,
-8 और -4 दोनों के चिन्ह ऋण हैं।
अतः -8 + (-4) = -(8 + 4)
Ans. -12
Q.2 (+8), (– 2) पूर्णांकों के युग्मों के योग ज्ञात कीजिए?
(A). 10
(B). -10
(C). 6
(D). -6
हल:- प्रश्नानुसार,
+8 और -2 के चिन्ह विपरीत हैं।
अतः +8 + (-2) = 8 – 2
Ans. 6
Q.3 (-12) में से 4 घटाइए?
(A). 4
(B). -4
(C). 16
(D). -16
हल:- प्रश्नानुसार,
4 का योज्य प्रतिलोम = – 4 हैं।
अतः -12 – 4
= -12 + (-4)
= -(12 + 4)
= -16
Ans. -16
Q.4 (-25) में से (-8) घटाइए?
(A). 8
(B). -8
(C). 17
(D). -17
हल:- प्रश्नानुसार,
-8 का योज्य प्रतिलोम = +8 हैं।
अतः -25 – (-8)
= -25 + (+8)
= -25 + 8
= -17
Ans. 17
Q.5 (-9) और (-4) के बीच में कितने पूर्णांक हैं?
(A). 6
(B). 8
(C). 4
(D). 10
हल:- प्रश्नानुसार,
-9 और -4 के बीच पूर्णांक -8, -7, -6 और -5 हैं।
अतः -9 और -4 के बीच 4 पूर्णांक हैं।
Q.6 परिकलित कीजिए?
1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10
(A). -2
(B). -3
(C). -5
(D). 5
हल:- प्रश्नानुसार,
1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10
= (1 + 3 + 5 + 7 + 9) – (2 + 4 + 6 + 8 + 1 + 0)
= 25 – 30
= -5
Ans. 5
Q.7 दो पूर्णांकों का योग 86 हैं। यदि इनमें से एक पूर्णांक –42 हैं। तो दूसरा पूर्णांक ज्ञात कीजिए?
(a). 155
(b). 123
(c). 111
(d). 128
हल:- प्रश्नानुसार,
दोनों पूर्णांकों का योग 86 हैं। इसलिए दूसरा पूर्णांक 86 में से (-42) घटाने पर प्राप्त होगा।
= 86 – (-42)
= 86 + 42
= 128
Ans. 128
Q.8 अंक 0, 1, 2, 3, 4, 5, 6, 7, 8 और 9 को इसी क्रम में लिखिए तथा इनके बीच में ‘+’ या ‘-‘ इस तरह रखिए कि 5 प्राप्त हों?
(a). 3
(b). 5
(c). 7
(d). 9
हल:- प्रश्नानुसार,
0 + 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9
= (0 + 1 + 3 + 5 + 7 + 9) – (2 + 4 + 6 + 8)
= 25 – 20
= 5
Ans. 5
Faq
Ans. धनात्मक, ऋणात्मक और शून्य से मिलकर बनी हुई संख्याएँ पूर्णांक संख्या कहलाती हैं।
Ans. सबसे छोटा पूर्णाक शून्य है।
Ans. (-7) और ० के बीच की संख्या = -6, -5, -4, -3, -2, -1,
∴ (-7) और 0 के बीच सबसे बड़ा पूर्णांक है (-1)।
Ans. पूर्णांक 16वीं शताब्दी के लैटिन शब्द से आया है जिसका अर्थ है “संपूर्ण” या “अक्षुण्ण”।
किसी संख्या को पूर्णांक मानने के लिए, वह पूर्ण होनी चाहिए – यहां कोई भिन्न या दशमलव नहीं है। एक पूर्णांक धनात्मक या ऋणात्मक हो सकता है।
Ans. 2 का सबसे बड़ा पूर्णांक फलन है वह 2 ही होगा।
Ans. Z = {⋯−4,−3,−2,−1,0,1,2,3,4…}. पूर्णांकों के समुच्चय के लिए अंकन Z जर्मन शब्द ज़हलेन से आया है, जिसका अर्थ है “संख्याएँ” । शून्य से बिल्कुल बड़े पूर्णांक धनात्मक पूर्णांक होते हैं और शून्य से बिल्कुल छोटे पूर्णांक ऋणात्मक पूर्णांक होते हैं।
उम्मीद हैं आपको पूर्णांक संख्याओं की जानकारी पसंद आयीं होगीं।
पूर्णांक संख्याओं से संबंधित किसी भी प्रश्न के लिए कमेंट करें धन्यवाद।