Class 4 Maths Solutions Chapter – 5

इस पेज पर आप Class 4 Maths Solutions Chapter – 5 पढ़ने वाले हैं तो आर्टिकल को पूरा जरूर पढ़िए।

पिछले पेज पर हमने Class 4 Maths Solutions Chapter – 1 की जानकारी शेयर की हैं तो उस पोस्ट को भी पढ़े।

चलिए आज हम Class 4 Maths Solutions Chapter – 5 की समस्त जानकारी पढ़ते और समझते हैं।

Class 4 Maths Solutions Chapter – 5

इस पेज पर आप पड़ेगें –

• भिन्न को किसी इकाई के भाग के रूप में समझना।
• भिन्न को एक जैसी इकाइयों के समूह के भाग के रूप में समझना।
• किसी समूह के भागों को सम भिन्न के रूप में दर्शाना।
• सम भिन्नों को बढ़ते एवं घटते क्रम में रखना।
• मिश्र भिन्न और विषम भिन्न को समझना।
• विषम भिन्न को मिश्र भिन्न में बदलना।
• मिस्र भिन्न को विषम भिन्न में बदलना।
• दो भिन्नों की तुलना करना।
• सरल सम भिन्नों को जोड़ना-घटाना जब हर समान हो।
• भिन्नों के जोड़ने व घटाने पर आधारित दैनिक जीवन की समस्याओं को हल करना।

भिन्नात्मक संख्याएँ

भिन्न को किसी इकाई के भाग के रूप में समझना।

किसी एक इकाई के दो बराबर भाग करने पर प्रत्येक भाग पूरी इकाई का 1/2 भाग कहलाता हैं।

यदि हम किसी इकाई के चार बराबर भाग करें तो प्रत्येक भाग पूरी इकाई का 1/4 भाग होगा।

यदि हम कुछ भाग की तुलना पूरी इकाई से करें।

जैसे किसी इकाई के चार बराबर भागों में से 3 भाग छायांकित करें।

तो छायांकित भाग सम्पूर्ण इकाई का 3/4 होगा।

3/4 छायांकित भाग, 1/4 शेष भाग

भिन्न 3/4 में 3 अंश और 4 हर हैं। या 4 बराबर किए भाग में से 3 भाग लेने पर हमें पूरी इकाई का 3/4 भाग प्राप्त होगा।

अभ्यास 5.1

1. निम्न चित्रों में छायांकित दिखाइए।

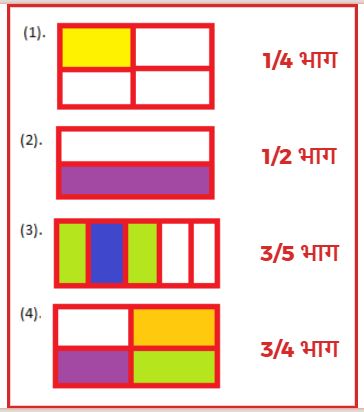
2. निम्न चित्रों में हर एक भाग के लिए भिन्न लिखिए?

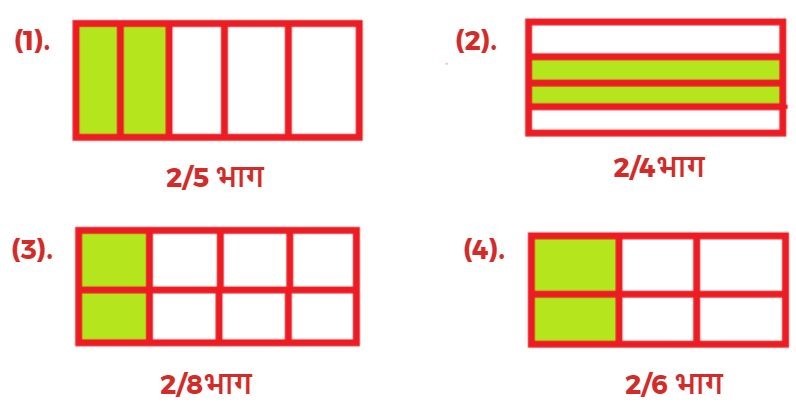
3. निम्न भिन्नों के लिए चित्र बनाइए?

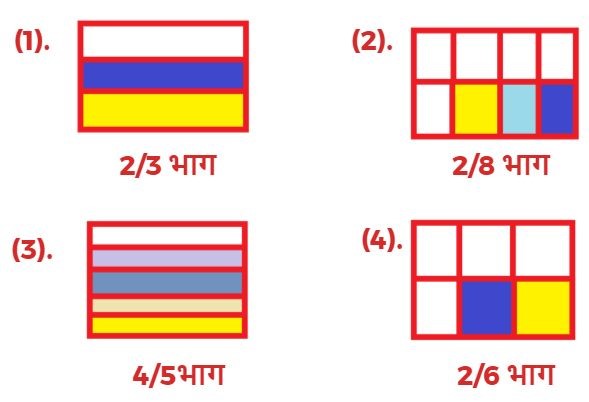
भिन्न को एक जैसी इकाइयों के समूह के भाग के रूप में समझना।

उदाहरण 1. इन 12 फूलों के समूह का 1/3 हिस्सा कितना होगा?

अतः 12 का 1/3 = 12 को 3 बराबर भागों में बांटकर 1 भाग लेना अतः 4 फूल आएंगे।

उदाहरण 2. इन 9 पत्तियों के समूह का 2/3 हिस्सा कितना होगा?

अतः 9 का 2/3 = 9 पत्तियों को 3 बराबर भाग में बांटने पर 1 भाग में 3 पत्तियाँ 2 भाग में 6 पत्तियाँ होगीं।

उदाहरण 3. इन 15 आकृतियों के समूह का 4/5 कितना होगा।

15 का 4/5 भाग करने के लिए हमने 15 को 5 बराबर भागों में बांटा।
प्रत्येक भाग में 3 आकृतियाँ आयीं।

इस तरह के 4 भाग लेने पर 3 + 3 + 3 + 3 = 12
अतः 15 का 4/5 भाग 12 हैं।

अभ्यास 5.2

1. चित्र बनाकर विभाजन कीजिए?

(1). 6 गेंदों के समूह का 1/2 हिस्सा।

6 का 1/2 भाग करने के लिए हमने 6 को 2 बराबर भागों में बांटा।
प्रत्येक भाग में 3 आकृतियाँ आयीं।

इस तरह के 2 भाग लेने पर 2 + 2 + 2 = 6
अतः 6 का 1/2 भाग 3 हैं।

(2). 4 पेंसिलों के समूह का 1/4 हिस्सा।

4 पेंसिलों का 1/4 भाग करने के लिए हमने 4 को 1 बराबर भागों में बांटा।
अतः 4 का 1/4 भाग 1 हैं।

(3). 8 टॉफियों के समूह का 2/4 हिस्सा।

8 का 2/4 भाग करने के लिए हमने 8 को 2 बराबर भागों में बांटा।
प्रत्येक भाग में 4 आकृतियाँ आयीं।

इस तरह के 4 भाग लेने पर 1 + 1 + 1 + 1 = 4
अतः 8 का 2/4 भाग 4 हैं।

(4). 15 तारों के समूह का 3/5 हिस्सा।

15 का 3/5 भाग करने के लिए हमने 15 को 5 बराबर भागों में बांटा।
प्रत्येक भाग में 3 आकृतियाँ आयीं।

इस तरह के 3 भाग लेने पर 3 + 3 + 3 = 9
अतः 15 का 3/5 भाग 9 हैं।

2. हल कीजिए?

(1). 16 का 1/2 = 8

(2). 16 का 1/4 = 4

(3). 10 का 1/5 = 2

(4). 18 का 1/3 = 6

3. निम्न में से कौन सी भिन्न किसी समूह जिसे 5 समान भागों में बांटा गया हैं तथा उसके 3 छायांकित भागों को दर्शाती हैं।

समान अंश वाली भिन्नों की तुलना करना।

भिन्न को अंश/हर के रूप में लिखते हैं।

यदि किसी इकाई के दो भिन्न के अंश समान हों।

जैसे : 1/4 और 1/6

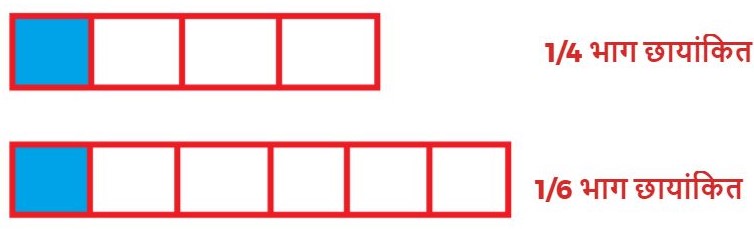
अतः 1/4 छायांकित भाग 1/6 छायांकित भाग से अधिक हैं।
अतः 1/4 और 1/6 में से 1/4 भिन्न बड़ी हैं।

Note :

चिन्ह > बड़ा हैं के लिए एवं चिन्ह < छोटा हैं के लिए उपयोग किया जाता हैं। खुले मुँह के तरफ की संख्या बड़ी होती हैं एवं बंद मुह के तरफ़ की संख्या छोटी होती हैं।

यदि भिन्नों के अंश समान हों और हर अलग-अलग हो तो जिस भिन्न का हर छोटा होगा। वह भिन्न बड़ी होगी।

उदाहरण 4. 2/4 और 2/7 में बड़ी भिन्न बताइए।

दोनों भिन्नों के छायांकित भाग की तुलना करने पर 2/4 छायांकित भाग वाली भिन्न बड़ी हैं।

अतः 2/4 > 2/7 से

2/4 और 2/7 को देखने पर दोनों भिन्न के अंश समान हैं अतः छोटे हर वाली भिन्न बड़ी होगीं।

उदाहरण 4. बढ़ते क्रम में लिखिए?

7/9, 7/2, 7/6

हल:- 7/9 < 7/6 < 7/2

उदाहरण 5. घटते क्रम में लिखिए?

5/9, 5/7, 5/8

हल:- 5/7 > 5/8 > 5/9

अभ्यास 5.3

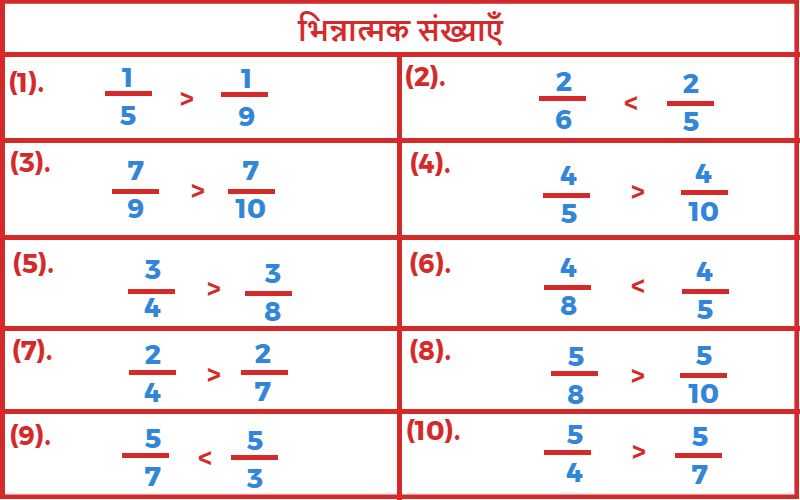
1. नीचे लिखी भिन्नों में से प्रत्येक में बड़ी भिन्न बताइए?

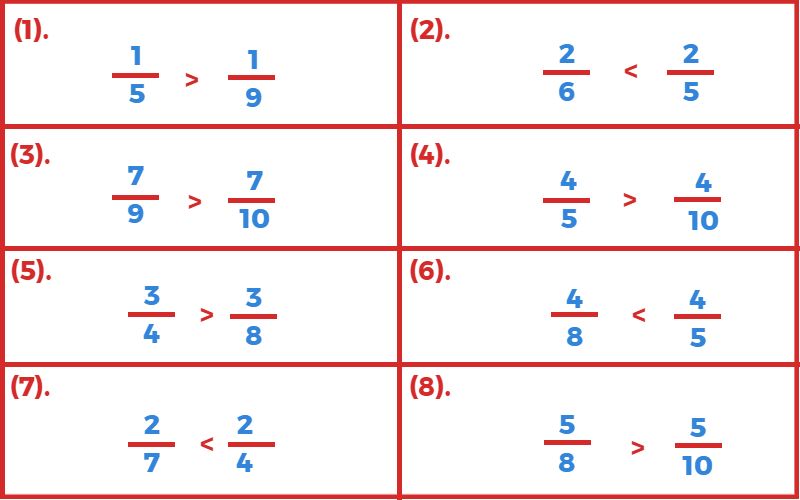
2. नीचे लिखी भिन्नों में छोटी भिन्न बताइए?

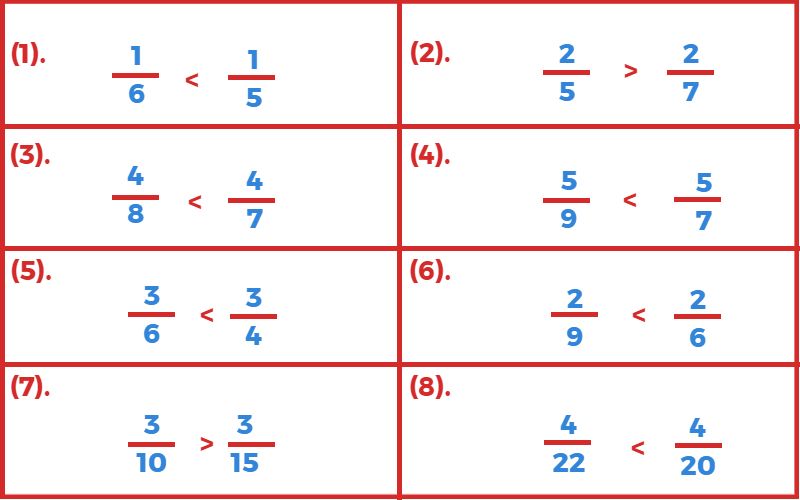
3. नीचे लिखी भिन्नों में छोटी (<) एवं बड़ी (>) का चिन्ह लगाइए?

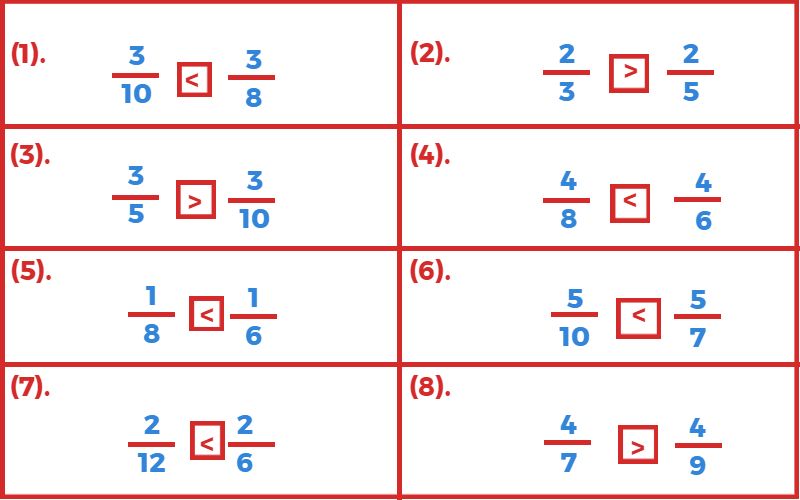
4. नीचे दी गई भिन्न को बढ़ते क्रम में लिखिए?

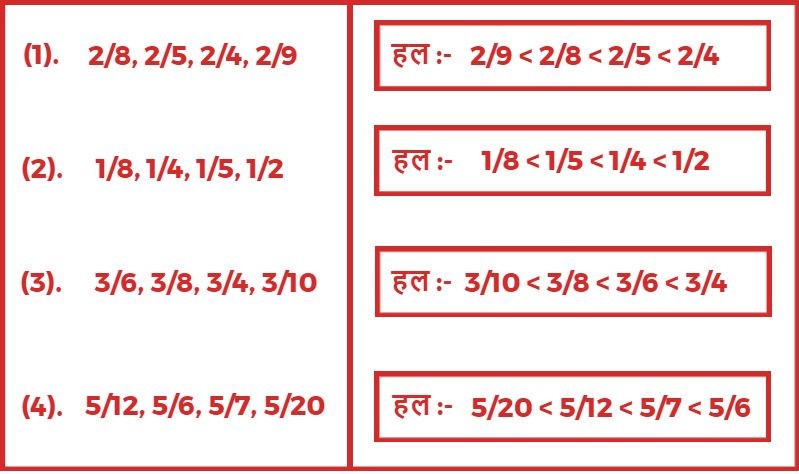
समान हर वाली भिन्नों की तुलना करना।

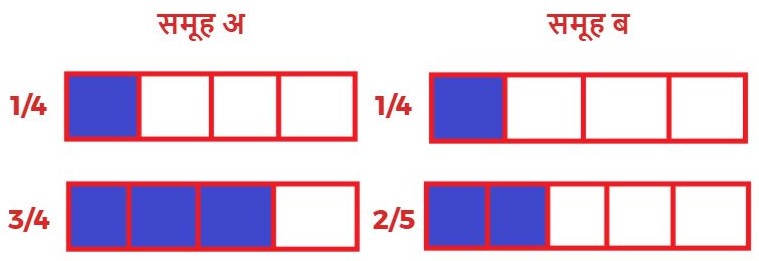
(समूह अ) के भिन्न 1/4 और 3/4 में दोनों भिन्नों की हर 4 हैं।

अतः दोनों समान हर वाली भिन्न हैं।

जबकि (समूह ब) के भिन्न 1/4 में हर 4, एवं 2/5 में हर 5 हैं।

अतः ये दोनों असमान हर वाली भिन्न हैं।

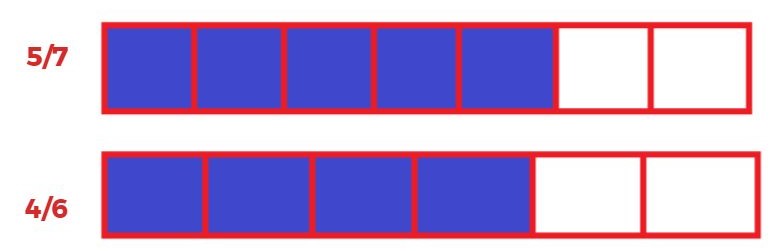
जैसे :- 5/7 और 4/6 में कौन बड़ा हैं।

हर समान होने पर जिस भिन्न का अंश बड़ा होगा। वह भिन्न बड़ी होगी।

अभ्यास 5.4

1. नीचे लिखी भिन्न में बड़ी भिन्न बताइए?

2. सत्य/असत्य लिखिए?

(1). समान हर वाली दो भिन्नों में बड़े अंश वाली भिन्न छोटी भिन्न होगीं।

Ans. असत्य

(2). 10/12 और 3/12 में 3/13 भिन्न बड़ी भिन्न हैं।

Ans. असत्य

(3). 3/5 > 4/5

Ans. असत्य

(4). 8/10 > 5/10

Ans. सत्य

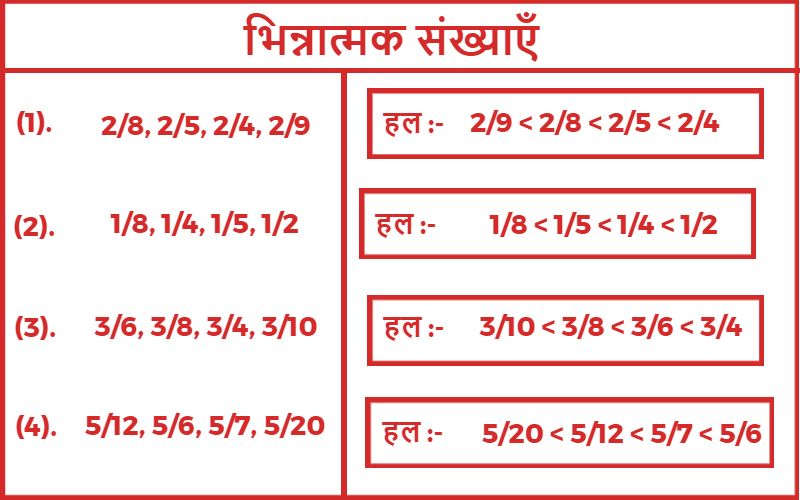
3. नीचे लिखे भिन्नों को बढ़ते क्रम में लिखिए?

4. नीचे लिखे भिन्नों को घटते क्रम में लिखिए?

समान हर वाले भिन्नों का जोड़

भिन्नों का जोड़ = अंशों का जोड़/हर

उदाहरण 6. 5/7 + 6/7

हल:- 5/7 + 6/7
(5 + 6)/7
11/7
Ans. 11/7

उदाहरण 7. 3/8 + 2/8 + 1/8
हल:- 3/8 + 2/8 + 1/8
= (3 + 2 + 1)/8
= 6/8

अभ्यास 5.5

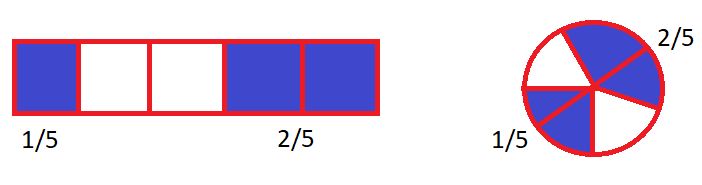
1. चित्रों को देखिए और खाली स्थान भरिए?

1/5 + 3/5 = 4/5

2/8 + 2/8 = 4/8

1/7 + 1/7 = 2/7

2/10 + 2/10 = 4/10

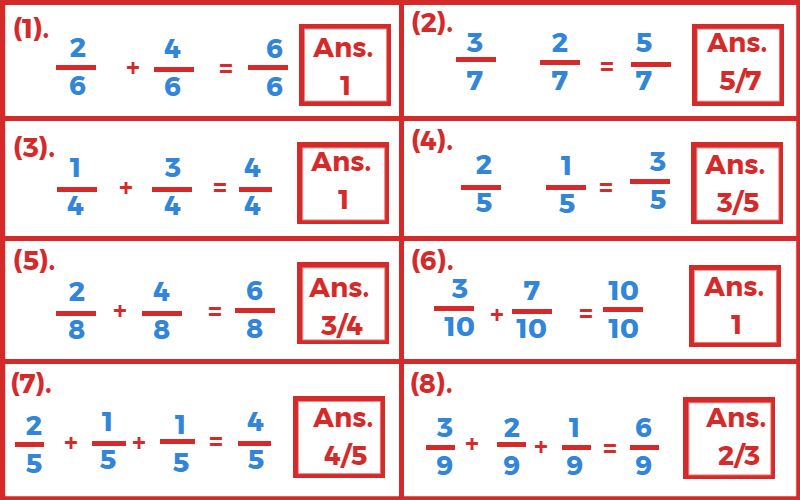
2. योगफल ज्ञात कीजिए?

समान हर वाले भिन्नों का घटाना

भिन्नों का अंतर = उनके अंशों का अंतर/हर

अभ्यास 5.6

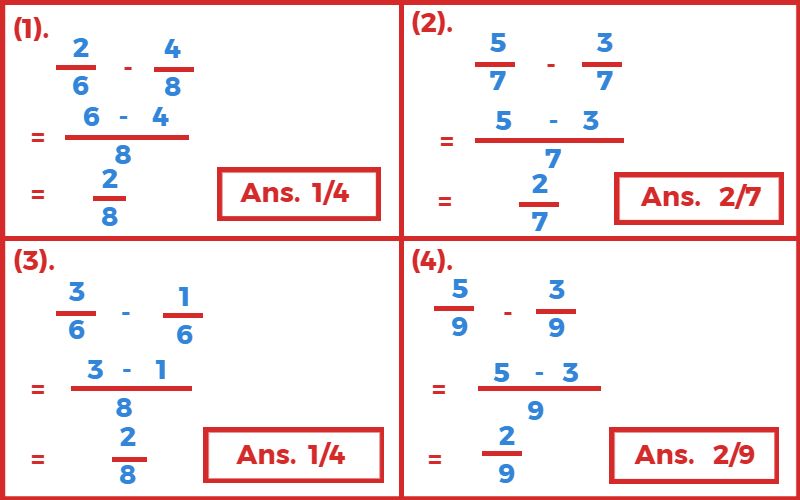
1. खाली स्थान भरिए?

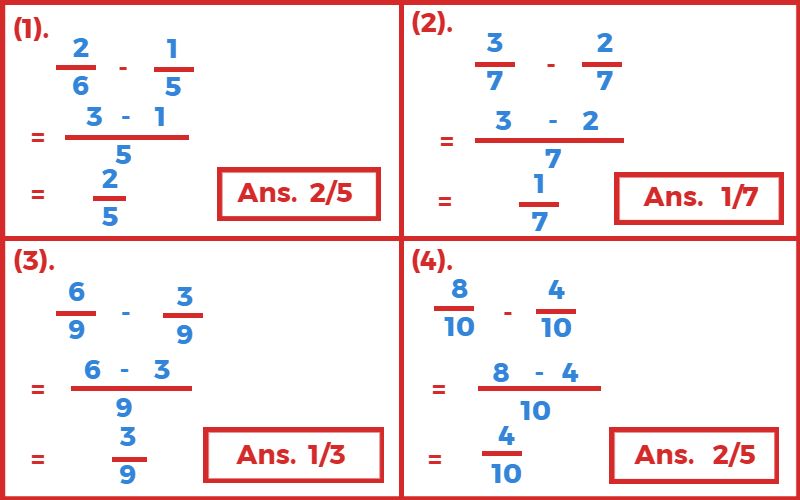
2. अंतर ज्ञात कीजिए?

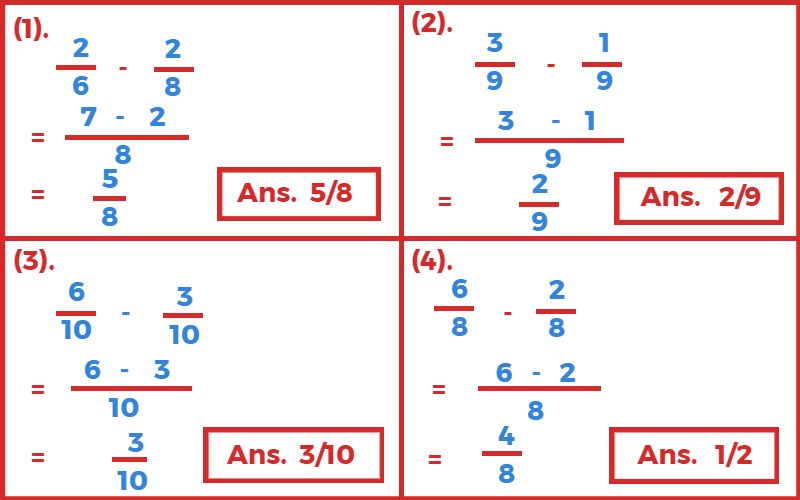
3. घटाइए?

किसी भिन्न के अंश और हर को समान संख्या से गुणा करने पर समतुल्य भिन्न प्राप्त होती हैं।

उदाहरण :-

1/2 = (1×2)/(2×2) = 2/4

1/2 = (1×3)/(2×3) = 3/6

1/2 = (1×4)/(2×4) = 4/8

1/2 = (1×5)/(2×5) = 5/10

उदाहरण 8. 2/5 की 4 समतुल्य भिन्ने बनाइए?

2/5 = (2×2)/(5×2) = 4/10

2/5 = (2×3)/(5×3) = 6/15

2/5 = (2×4)/(5×4) = 8/20

2/5 = (2×5)/(5×5) = 10/25

अतः दी हुई भिन्न 2/5 की समतुल्य भिनें 4/10, 6/15,8/20, 10/25 हैं।

अभ्यास 5.7

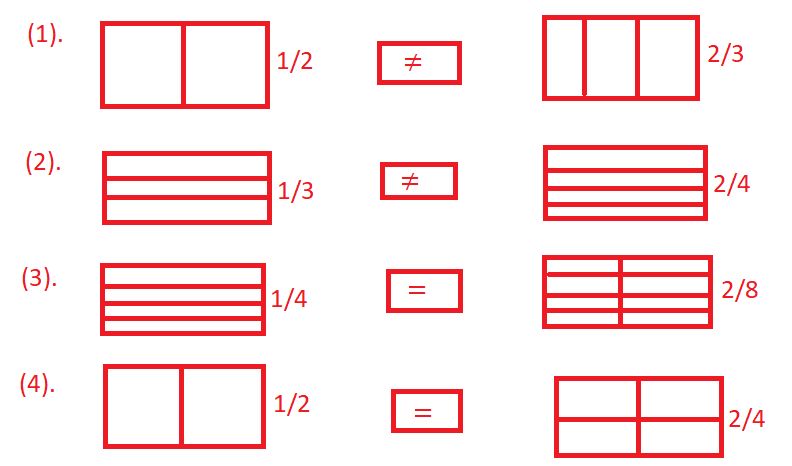
1. चित्रों में बनी हुई दो भिन्न तुल्य हैं या नहीं। प्रत्येक के लिए बराबर (=) या बराबर नहीं (≠) बॉक्स में लिखिए?

2. दी गई भिन्न के समतुल्य भिन्न पर गोला लगाइए?

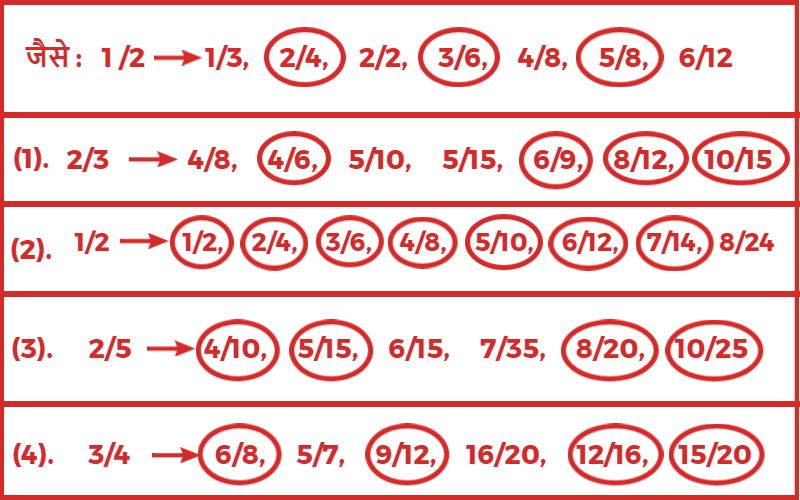
3. निम्न भिन्न के लिए अंश और हर में एक ही संख्या का गुणा करके 4 तुल्य भिन्ने बनाइए?

जैसे :- 1/3 → 1/3 × 2/2 = 2/6, 1/3 × 3/3 = 3/9, 1/3 × 4/4 = 4/12, 1/3 × 5/5 = 5/15

(1). 3/5 → 3/5 × 2/2 = 6/10, 3/5 × 3/3 = 9/15, 3/5 × 4/4 = 12/20, 3/5 × 5/5 = 15/25

(2). 4/5 → 4/5 × 2/2 = 8/10, 4/5 × 3/3 = 12/15, 4/5 × 4/4 = 16/20, 4/5 × 5/5 = 20/25

(3). 5/6 → 5/6 × 2/2 = 10/12, 5/6 × 3/3 = 15/18, 5/6 × 4/4 = 20/24, 5/6 × 5/5 = 25/30

(4). 5/7 → 5/7 × 2/2 = 10/14, 5/7 × 3/3 = 15/21, 5/7 × 4/4 = 20/28, 5/7 × 5/5 = 25/35

सम भिन्न, विषम भिन्न और मिश्र भिन्न

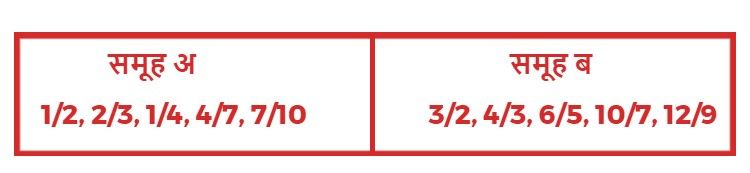
• समूह अ में प्रत्येक भिन्न का अंश अपने हर से छोटा हैं।
• समूह ब में प्रत्येक भिन्न का अंश अपने हर से बड़ा हैं।

सम भिन्न : वह भिन्न जिसका अंश, हर से छोटा होता हैं। उसे सम भिन्न कहते हैं।

विषम भिन्न : वह भिन्न जिसका अंश, हर से बड़ा होता हैं उसे विषम भिन्न कहते हैं।

• समूह अ की सभी भिन्न सम भिन्न हैं।
• समूह ब की सभी भिन्न विषम भिन्न हैं।

अभ्यास 5.8

1. निम्लिखित में कौन सी सम भिन्न हैं?

2. निम्लिखित में कौन सी विषम भिन्न हैं?

3. निम्न में कौन सी मिश्र भिन्न हैं?

मिश्र भिन्न को विषम भिन्न में बदलना

5 + 3/8
5 को भिन्न के रूप में लिखिए।
5/1 = (5×8)/(1×8)
= (5×8)/8
5 + 3/8 = (5 × 8)/8 + 3/8
= (5 × 8 + 3)/8
= (40 + 3)/8
= 43/8

(1). सबसे पहले 8 का 5 से गुणा करते हैं।
8 × 5 = 40
(2). इस गुणनफल 40 में 3 को जोड़ते हैं।
40 + 3 = 43
(3). इस प्रकार भिन्न बन जाती हैं। 43/8
(4). 43/8 एक विषम भिन्न हैं।

अब 3 + 4/5 को विषम भिन्न में बदलकर देखें।

(1). पहले 5 × 3 = 15
(2). 15 + 4 = 19
(3). अतः 3 + 4/5 = 19/5

अभ्यास 5.9

1. दी हुई भिन्नों को मिश्र भिन्न में बदलिए?

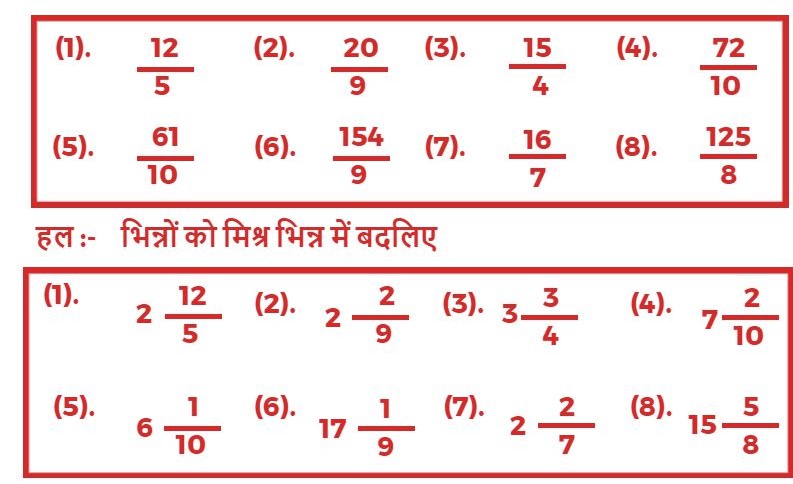
2. मिश्र भिन्नों को विषम भिन्न में बदलिए?

जरूर पढ़िए :

• Class 4 Maths Solutions Chapter – 1
• Class 4 Maths Solutions Chapter – 2
• Class 4 Maths Solutions Chapter – 3
• Class 4 Maths Solutions Chapter – 4

उम्मीद हैं आपको Class 4 Maths Solutions Chapter – 5 की जानकारी पसंद आयी होगीं।