इस पेज पर आप प्रायिकता की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।
पिछले पेज पर हमने ज्यामिति की जानकारी शेयर की हैं तो उस पोस्ट को भी पढ़े।
चलिए आज हम प्रायिकता की समस्त जानकारी को पढ़ते और समझते हैं।
Table of Contents
प्रायिकता किसे कहते है
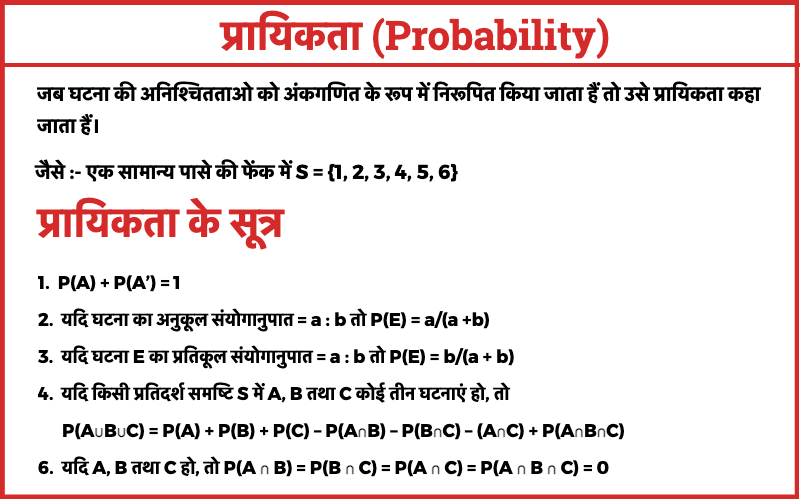
जब घटना की अनिश्चितताओ को अंकगणित के रूप में निरूपित किया जाता हैं तो उसे प्रायिकता कहा जाता हैं।
प्रायिकता को अंग्रेजी में Probability कहते है।
किसी घटना के होने की सम्भावना को प्रायिकता या संभाव्यता कहते हैं।
जैसे :- एक सामान्य पासे की फेंक में S = {1, 2, 3, 4, 5, 6}
घटना :- प्रतिदर्श समष्टि के प्रत्येक उपसमुच्च्य को एक घटना कहते हैं इसे साधारण रूप में E से सूचित किया करते हैं।
जैसे :- एक सिक्के की उछाल में S {H, T}
यदि शीर्ष ऊपर आने की घटना E हो, तो E = {H} ⊆ S
यदि S प्रतिदर्श समष्टि हो, तो किसी घटना E की प्रायिकता P(E) = n(E)/n(S)
जहाँ n(E) = समुच्चय E के अवयवों की संख्या
n(E) = प्रतिदर्श समष्टि S के अवयवों की संख्या
दूसरे शब्दों में,
P(E) = (E के पक्ष में तरीके)/कुल तरीके
जैसे :- यदि एक पासा फेंका जाए, तो चूंकि पासे पर 6 अंक लिखे रहते हैं तथा इनमें से कोई भी अंक ऊपर आ सकता हैं।
- अतः प्रतिदर्श समष्टि S में अवयवों की संख्या = n(S) = 6
- अब संख्या 3 के ऊपर आने की घटना यदि E हो, तो n(E) = 1
- अतः ऊपर अंक 3 के आने की प्रायिकता P(E) = n(E)/n(S) = 1/6
किसी घटना में अवयवों की संख्या ज्ञात करना
1. गिनती का योग नियम :- यदि E एक घटना है जो घटना E₁ या E₂ में से किसी एक के घटाने से घटती हैं।
n(E) = n(E₁) + n(E₂)
2. गिनती का गुणन नियम :- यदि E एक घटना है, जो घटना E₁ एवं E₂ दोनों के एक साथ घटाने से घटती हैं।
n(E) = n(E₁) × n(E₁)
3. क्रमचय :- यदि कोई घटना E तभी घटित होती हैं, जब n विभिन्न वस्तुओं में r वस्तुएं सजाई जाती हैं।
n(E) = ⁿPᵣ = n!/(n – r)!
4. संचय :- यदि कोई घटना E तभी घटित होती हैं, जब n विभिन्न वस्तुओं में से r वस्तुएं चुनी जाती हैं।
n(E) = ⁿCᵣ = n!/r!( n – r)!
जरूर पढ़िए : क्रमचय और संचय की परिभाषा
परस्पर अपवर्जी घटनाएं
किसी प्रतिदर्श समष्टि की दो घटनाएं E₁ तथा E₂ एक साथ नहीं घटित होती हैं तो इन घटनाओं को परस्पर अपवर्जी घटनाएं कहाँ जाता हैं, जिसमें E₁ ∩ E₂ = ∅ होता हैं।
जब E₁ और E₂ दो परस्पर अपवर्जी घटनाएं हैं तो घटना (E₁ या E₂) की प्रायिकता निम्न प्रकार से मालूम किया जा सकता हैं।
P(E₁ ∩ E₂) = P(E₁) + P(E₂)
लेकिन जब E1 तथा E2 दो परस्पर अपवर्जी घटनाएं नहीं हों, तो घटना (E₁ या E₂) की प्रायिकता निम्न प्रकार से मालूम किया जा सकता हैं।
P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
स्वतंत्र घटना
यदि दो घटनाओं का घटित होना या नहीं घटित होना एक दूसरे पर निर्भर न हो, तो उन्हें स्वतंत्र घटनाएं कहते हैं।
दूसरे शब्दों में, घटनाओं A और B स्वतंत्र होंगी यदि P(A ∩ B) = P(AB) = P(A)P(B)
जैसे यदि एक सिक्के को दो बार उछाला जाए, तो पहली बार शीर्ष का आना दूसरी बार शीर्ष के आने से स्वतंत्र हैं।
परतंत्र घटना
यदि एक घटना का घटित होना दूसरी घटना पर निर्भर हो, तो ऐसी घटनाओं को परतंत्र घटनाएं कहते हैं।
जैसे ताश की एक गड्डी से एक पत्ता खींचा जाता हैं जिसे बाहर रखते हुए यदि दूसरा पत्ता खींचा जाए तो दूसरे पत्ते का निकला पहले पर निर्भर करेगा यानी पहले और दूसरे पत्ते का खींचा जाना परतंत्र घटनाएं हैं।
प्रतिबन्धी प्रायिकता
यदि प्रतिदर्श समष्टि में दो घटनाएं A और B इस तरह हों कि A के घटने के बाद ही B घटती हो, तो A घटने के बाद B के घटने की इस प्रायिकता को P(B/A) लिखते हैं तथा इसे, इस प्रतिबन्ध पर कि A घट चुकी हैं, B की प्रतिबन्धी प्रायिकता कहते हैं।
P(B/A) = P(A ∩ B) / P(A)
जैसे :- दो पासों के फैंकने के क्रम में यदि A = पहले पासे पर 3 आने की घटना तथा B = दोनों पासों पर आई संख्याओ का योग 7 होने की घटना हो, तो B की प्रायिकता B की प्रतिबन्धी प्रायिकता होगी इस प्रतिबन्धी पर कि घटना A घट चुकी हैं।
प्रायिकता के सूत्र
1. P(A) + P(A’) = 1
जहाँ A कोई घटना हैं तथा A’ इसकी पूरक घटना हैं।
- घटना का अनुकूल संयोगानुपात E = P(E) : P(E’)
- घटना का प्रतिकूल संयोगानुपात E = P(E’) : P(E)
2. यदि घटना का अनुकूल संयोगानुपात = a : b तो P(E) = a/(a +b)
3. यदि घटना E का प्रतिकूल संयोगानुपात = a : b तो P(E) = b/(a + b)
4. यदि किसी प्रतिदर्श समष्टि S में A, B तथा C कोई तीन घटनाएं हो, तो
P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(B∩C) – (A∩C) + P(A∩B∩C)
5. यदि A, B तथा C हो, तो P(A ∩ B) = P(B ∩ C) = P(A ∩ C) = P(A ∩ B ∩ C) = 0
तथा P(A ∪ B ∪ C) = P(A) + P(B) + P(C)
ताश तथा ब्रिज से सम्बंधित महत्वपूर्ण बिन्दु
- ताश की एक गद्दी में 52 पत्ते होते हैं।
- ताश की गद्दी में 26 लाल और 26 काले रंग के पत्ते होते हैं।
- 26 लाल रंग के पत्तों में से 13 लाल पान के और 13 ईंट के पत्ते होते हैं।
- 26 काले रंग के पत्तों में से 13 काले पान के और 13 चिड़िया के पत्ते होते हैं।
- लाल पान, ठीकरी, काला पान चिड़िया में से प्रत्येक में एक-एक छक्का होता हैं अर्थात ताश की गद्दी में कुल चार छक्के होते है। इसी प्रकार चार बादशाह चार बेगम और चार गुलाम होते हैं।
- ब्रिज के खेल में चार खिलाड़ी होते हैं और प्रत्येक को 13 पत्ते मिलते हैं ब्रिज के खेल में प्रेत्यक रंग के लिए 5 पत्ते होते हैं।
प्रायिकता के सवाल
Q.1 एक सिक्के को उछालने पर टेल आने की प्रायिकता क्या हैं?
A. 1/2
B. 1
C. 2/1
D. 2
हल:- प्रश्नानुसार,
एक सिक्के में Head और Tail होते हैं।
सिक्के के उछाल में Head आने की प्रायिकता
S = {H, T},
E = {T}
P(E) = n(E)/n(S)
P(E) = 1/2
Ans. 1/2
Q.2 एक साधारण पासे को फेंका जाता हैं बताइए कि चार का अंक ऊपर आए।
A. 1/4
B. 1/6
C. 1/2
D. 1/8
हल:- प्रश्नानुसार,
पासे पर 1, 2, 3, 4, 5, 6 तक अंक होते हैं जिनमें से किसी भी एक के ऊपर आने की संभावना समान हैं।
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
माना कि,
E = {4 का अंक ऊपर आने की घटना}
n(E) = 1
अतः घटना E की संभाविता P(E) = n(E)/n(S) = 1/6
Ans. 1/6
Q.3 यदि एक पासे को 30 बार फेंका जाए तो कितने बार 2 के आने की प्रायिकता हैं?
A. 2 बार
B. 5 बार
C. 3 बार
D. 9 बार
हल:- प्रश्नानुसार,
पासे को एक बार फेंके जाने पर 2 अंक आने की प्रायिकता = 1/6
पासे की प्रत्येक फेंक परस्पर अपवर्जी हैं।
तो 30 बार पासे फेंके जाने पर 2 आने की प्रायिकता
= 1/6 + 1/6 + 1/6 + …….. 30
= 5 बार
Ans. 5 बार
Q.4 एक पर्स में 5 चांदी के एवं 2 सोने के सिक्के हैं एक दूसरे पर्स में 4 चांदी के और 3 सोने के सिक्के हैं किसी एक पर्स से एक सिक्का निकाला गया इसे चांदी का सिक्का होने की क्या प्रायिकता हैं?
A.19/47
B. 17/42
C. 9/49
D. 20/49
हल:- प्रश्नानुसार,
पहले पर्स से 1 सिक्का निकालने पर चाँदी होने की संभावना = 5/7
दूसरे पर्स से 1 सिक्के निकालने पर चाँदी होने की संभावना = 4/7
संयुक्त रूप से चांदी होने की संभावना = (5×4)/(7×7)
= 20/49
Ans. 20/49
Q.5 20 हरा और 15 लाल गेंद एक बर्तन में डाले जाते हैं एक हरा गेंद को चुनने की संभावना कितनी हो सकती हैं?
A. 3/7
B. 3/7
C. 4/7
D. 5/7
हल:- प्रश्नानुसार,
कुल गेंद = 20 + 15
एक हरा गेंद चुनने की संभावना
²⁰C₁, ³⁵C₁
= ²⁰C₁ / ³⁵C₁
= 20/35
= 4/7
Ans. 4/7
Q.6 एक दर्जन संतरे वाले एक डिब्बे में एक तिहाई संतरे खराब हो गए हैं यदि इस डिब्बे में से किसी भी तीन संतरों को बाहर निकाला जाता हैं, तो निकाले गए इन तीन संतरों में से कम से कम एक संतरा अच्छा होगा, इसकी संभावना कितनी हैं?
A. 54/55
B. 45/55
C. 1/55
D. 3/55
हल: प्रश्नानुसार,
तीन संतरे निकालने के कुल प्रकार = ¹²C₃
= (12 × 11 × 10)/(3 × 2 × 1)
= 220
खराब संतरे = 12 × 1/3
= 4 संतरे
एक भी अच्छा संतरा नहीं होने का कुल प्रकार = ⁴C₃
= (4 × 3 × 2)/(3 × 2)
= 4
कम से कम एक अच्छा संतरा होने की प्रायिकता = 1 – ⁴/₂₂₀
= (220 – 4)/220
= 54/55
Ans. 54/55
Q.7 52 पत्तों की एक गद्दी में से दो पत्ते निकाले गए, तो निकाले गए पत्ते दो इक्के होंगे इसकी क्या संभावना हैं?
A. 2/245
B. 1/218
C. 4/1569
D. 1/221
हल: प्रश्नानुसार,
52 से 2 पत्ते निकालने के कुल प्रकार = ⁵²C₂
= (52 × 51)/2 × 1
= 1326
4 में से दो इक्के निकालने के कुल प्रकार = ⁴C₂
= (4 × 3)/(2 × 1)
= 12/2
= 6
दो इक्के होने की संभावना
= 6/1326
= 1/221
Ans. 1/221
Q.8 तीन सिक्के उछाले जाते हैं, कम से कम एक चित्त आने की क्या प्रायिकता हैं?
A. 1/8
B. 1/2
C. 7/8
D. 1/3
हल: प्रश्नानुसार,
तीन सिक्के उछाले जाने पर कुल घटनाएं = 2
= 8
कम से कम 1 चित्त (Head) आने की अनुकूल घटनाएं = {HTT, THT, TTH, HHT, HTH, TTH, HHH}
= 7
अभीष्ट प्रायिकता = 7/8
Ans. 7/8
Q.9 A 75% मामलों में सच बोलता हैं तथा B 60% मामलों में सच बोलते हैं दोनों का विरोधाभास होने की संभावना ज्ञात करें?
A. 25%
B. 75%
C. 45%
D. 84%
हल: प्रश्नानुसार,
A की सच बोलने की संभावना = 74/100
= 3/4
A के छूट बोलने की संभावना = 1 – 3/4
= 1/4
B के सच बोलने की संभावना = 60/100
= 3/5
B के झूठ बोलने की संभावना = 1 – 3/5
= 2/5
विरोधाभास तभी होगा जब एक बोलता हो तथा दूसरा झूठ,
अतः ऐसी संभावना = (3 × 2 × 1 × 3 × 9 × 100)/(4 × 5 × 4 × 4)
= 45%
Ans. 45%
Q.10 LEADER शब्द के अक्षरों को कितने विविध प्रकार से व्यवस्थित किया जा सकता हैं?
A. 360
B. 560
C. 430
D. 600
हल: प्रश्नानुसार,
अभीष्ट प्रकार = 6!/2!
(6 × 5 × 4 × 3 × 2 × 1) / (2 × 1)
= 360
Ans. 360
Q.11 स्वरों को हर बार साथ रखकर एवं वयंजन को भी हर बार साथ रखकर ORGANISE शब्द को अलग-अलग कितने प्रकार से क्रमबद्ध किया जा सकता हैं?
A. 900
B. 720
C. 576
D. 300
हल: प्रश्नानुसार,
कुल शब्द = 8,
स्वर = 4,
व्यंजक = 4
अभीष्ट प्रकार = (4! × 4!)
= 4 × 3 × 2 × 1 × 4 × 3 × 2 × 1
= 576
Q.12 शब्द DESIGN के अक्षरों को अलग-अलग कितनी तरह से क्रमबद्ध किया जा सकता हैं कि कोई भी वयंजन दो में से किसी भी छोर पर न हो?
A. 20
B. 56
C. 60
D. 48
हल: प्रश्नानुसार,
DESIGN में कुल 6 अक्षर हैं
कुल शब्द = 6, व्यंजक = 4
अभीष्ट प्रकार = 2 × 4!
= 2 × 4 × 3 × 2 × 1
= 48
Ans. 48
FAQ
Ans. किसी घटना के होने की सम्भावना को प्रायिकता या संभाव्यता कहते हैं। सांख्यिकी, गणित, विज्ञान, दर्शनशास्त्र आदि क्षेत्रों में इसका बहुतायत से प्रयोग होता है।
Ans. यदि A तथा B दो घटनाएँ हैं तो P(AUB) या P (A + B) का अर्थ A घटित होने या B घटित होने या दोनों का एक साथ घटित होने की प्रायिकता होता है। इसका अर्थ, दो घटनाओं, A तथा B, में से कम से कम एक के घटने की प्रायिकता भी होता है ।
Ans. यदि A तथा B दो घटनाएँ हैं तो P(AUB) या P (A + B) का अर्थ A घटित होने या B घटित होने या दोनों का एक साथ घटित होने की प्रायिकता होता है।
Ans. किसी घटना के घटित होने की संभावना का एक संख्यात्मक माप।
Ans. संभाव्यता 4 प्रमुख प्रकार की होती है।
शास्त्रीय संभाव्यता, अनुभवजन्य संभाव्यता, व्यक्तिपरक संभाव्यता, स्वयंसिद्ध संभाव्यता। किसी घटना की संभावना उसके घटित होने की संभावना है।
उम्मीद हैं आपको प्रायिकता की जानकारी पसंद आयी होगीं। यदि आपको यह जानकारी पसंद आयी हो तो इस आर्टिकल को अपने दोस्तों के साथ जरूर शेयर कीजिए धन्यवाद।