इस पेज पर आप थेल्स प्रमेय की समस्त जानकारी पढ़ने वाले हैं तो आर्टिकल को पूरा पढ़िए।
पिछले पेज पर हमने त्रिकोणमिति की जानकारी शेयर की हैं तो उस पोस्ट को भी जरूर पढ़े।
चलिए इस पेज पर थेल्स प्रमेय की समस्त जानकारी को पढ़ते और समझते हैं।
थेल्स प्रमेय का कथन
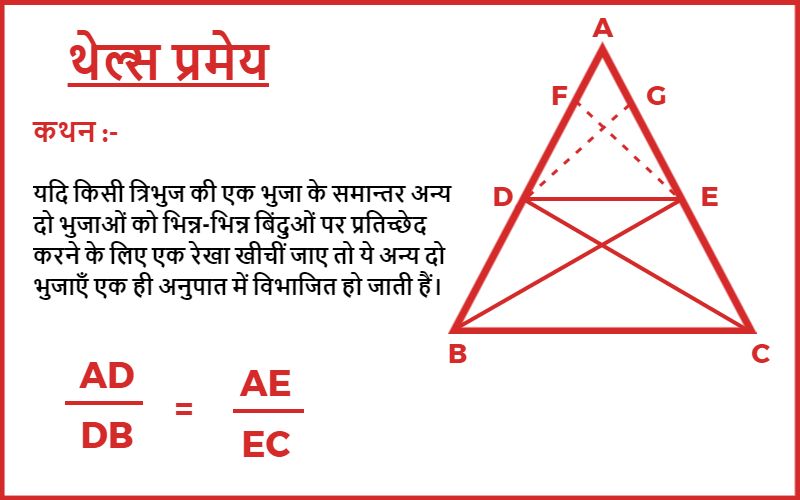
यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करने के लिए एक रेखा खीचीं जाए तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
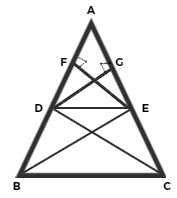
दिया हैं :-
∆ABC में DE ∥ BC तथा DE, भुजाओं AB और AC को क्रमशः D और E पर काटती हैं।
सिद्ध करना हैं :-
AD/DB = AE/EC
रचना :-
BE और CD को मिलाया तथा DG ⊥ AC
तथा EF ⊥ AB खींचा।
उपपत्ति :-
∆ADE व ∆DBE में
त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
ar∆ADE = ½ × AD × EF ……….(i)
ar∆DBE = ½ × DB × EF ……….(ii)
समीकरण (1) में समीकरण (2) का भाग देने पर
ar∆ADE/ar∆DBE = (½ × AD × EF)/(½ × DB × EF)
ar∆ADE/ar∆DBE = AD/DB ……….(iii)
अब ∆ADE और ∆ECD में,
ar(∆ADE) = ½ × AE × DG ……….(iv)
ar(∆ECD) = ½ × EC × DG ……….(v)
समीकरण (iv) में समीकरण (v) का भाग देने पर,
ar(∆ADE)/ar(∆ECD) = (½ × AE × DG )/(½ × EC × DG)
ar(∆ADE)/ar(∆ECD) = AE/EC …………..(vi)
ar(∆ADE)/ar(∆DBE) = AE/EC …………..(vii)
समीकरण (iii) व समीकरण (vi) से,
AD/DB = AE/EC
यही सिद्ध करना था।
उम्मीद हैं आपको थेल्स प्रमेय की जानकारी पसंद आयीं होगीं।
थेल्स प्रमेय की जानकारी अपने दोस्तों के साथ शेयर जरूर कीजिए।