इस पेज पर आप बेलन की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।
पिछले पेज पर हमने शंकु की जानकारी शेयर की हैं तो उस पोस्ट को भी पढ़े।
चलिए आज हम बेलन की परिभाषा, बेलन का सूत्र और उदाहरण की समस्त जानकारी को पढ़ते और समझते हैं।
बेलन क्या हैं
बेलन ज्यामिति में एक त्रिआयामी ठोस की आकृति है। इसका पार्श्व पृष्ठ वक्र, सिरे समान त्रिज्या के वृत्ताकार होते हैं, बेलन सरल रूप में एक रोलर या समान व्यास का गिलास है।
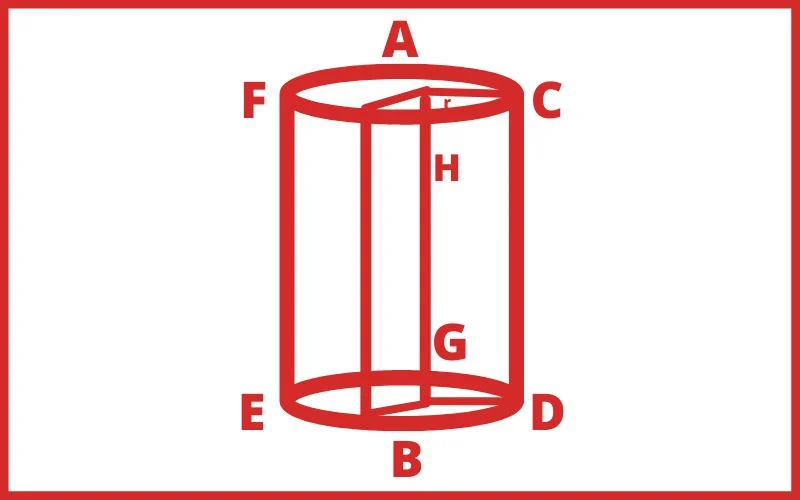
किसी वृत्त की परिधि पर लम्ब रूप से हमेशा अपने ही समांतर किसी सरल रेखा के घूमने से जिस पिण्ड का निर्माण होता हैं उसे बेलन कहते हैं।
बेलन के सूत्र
- बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई
= πr²h - बेलन का वक्रप्रष्ठ = आधार की परिमाप × ऊँचाई = 2πrh
- बेलन का सम्पूर्ण प्रष्ठ = वक्रप्रष्ठ का क्षेत्रफल + 2 × आधार का क्षेत्रफल = 2πrh + 2πr²
= 2πr(r + h) - खोखले बेलन का आयतन = πh(r₁² – r₂²)
- खोखले बेलन का वक्रप्रष्ठ = 2πh(r₁² + r₂²)
- खोखले बेलन का सम्पूर्ण प्रष्ठ = 2πh(r₁ + r₂) + 2π(r₁² – 2r₂²)
बेलन के सवाल
Q.1 एक बेलन की ऊँचाई 80 सेंटीमीटर तथा उसके आधार का व्यास 7 सेंटीमीटर हैं। बेलन के सम्पूर्ण प्रष्ठ का क्षेत्रफल क्या हैं?
A. 1873 वर्ग सेंटीमीटर
B. 183.7 वर्ग सेंटीमीटर
C. 817.3 वर्ग सेंटीमीटर
D. 1837 वर्ग सेंटीमीटर
हल:- प्रश्नानुसार,
बेलन के सम्पूर्ण प्रष्ठ का क्षेत्रफल = 2πr(r + h)
= 2 × 22/7 × 7/2(7/2 + 80)
= 1837
Ans. 1837 वर्ग सेंटीमीटर
Q.2 समबेलन की सम्पूर्ण सतह क्या होगी। यदि ऊँचाई 5 सेंटीमीटर और आधार का क्षेत्रफल 616 वर्ग सेंटीमीटर हो?
A. 1672 वर्ग सेंटीमीटर
B. 1432 वर्ग सेंटीमीटर
C. 1345 वर्ग सेंटीमीटर
D. 1476 वर्ग सेंटीमीटर
हल:- प्रश्नानुसार,
माना आधार की त्रिज्या = r सेंटीमीटर
πr² = 616
r² = 616/π
= (616 × 7)/22
= 28 × 7
r = √28 × 7
r = 14
सम्पूर्ण सतह = 2πr (r + h) वर्ग सेंटीमीटर
= 2 × 22/7 × 14(14 + 5)
= 2 × 22 × 2 × 19
= 1672
Ans. 1672 वर्ग सेंटीमीटर
Q.3 एक बेलन का वक्रप्रष्ठ 264 वर्ग मीटर हैं। उसका आयतन 924 घन मीटर हैं। तो बेलन की ऊँचाई हैं?
A. 4 मीटर
B. 6 मीटर
C. 8 मीटर
D. 10 मीटर
हल:- बेलन का वक्रप्रष्ठ = 2πrh
प्रश्नानुसार,
264 = 2 × 22/7 × rh
rh = 42
πr²h = 924
r = 7
h = 6 मीटर
Ans. 6 मीटर
Q.4 2 सेंटीमीटर भुजा के लकड़ी का एक घन हैं। यदि इसमें अधिकतम आयतन का बेलन काटा जाए तो शेष बची हुई लकड़ी का आयतन कितना होगा?
A. 9/7 घन सेंटीमीटर
B. 10/7 घन सेंटीमीटर
C. 11/7 घन सेंटीमीटर
D. 12/7 घन सेंटीमीटर
हल:- प्रश्नानुसार,
बेलन की ऊँचाई = 2 सेंटीमीटर
त्रिज्या = 1 सेंटीमीटर
घन का आयतन = 2³
= 8 घन सेंटीमीटर
बेलन का आयतन = 22/7 × 1 × 1 × 2
= 44/7 घन सेंटीमीटर
शेष लकड़ी का आयतन = 8 – 44/7
= (56 – 44)/7
= 12/7 घन सेंटीमीटर
Ans. 12/7 घन सेंटीमीटर
Q.5 दो बेलनों के आधारों की त्रिज्याओं का अनुपात 2 : 3 हैं तथा उनकी ऊंचाइयों का अनुपात 5 : 3 हैं। इनके आयतनों का अनुपात क्या होगा?
A. 27 : 20
B. 20 : 27
C. 4 : 9
D. 9 : 4
हल:- माना, बेलनों की त्रिज्याएँ क्रमशः 2r तथा 3r हैं।
ऊँचाई 5h तथा 3h हैं।
आयतनों का अनुपात = π(2r)² × 5h/π(3r)² × 3h
= 20 : 27
Ans. 20 : 27
उम्मीद हैं आपको बेलन की पोस्ट पसंद आयी होगीं
यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ शेयर कीजिए

