वृत्त की परिधि की परिभाषा, सूत्र और उदाहरण

इस पेज पर आप वृत्त की परिधि की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।

पिछले पेज पर हमने वृत्त और गोला की जानकारी शेयर की हैं तो उस पोस्ट को भी पढ़े।

चलिए आज हम वृत्त की परिधि की समस्त जानकारी को पढ़ते और समझते हैं।

वृत्त की परिधि की परिभाषा

वृत्त और दीर्घवृत्त के बाहरी घेरे और घेरे की लम्बाई को परिधि कहते हैं। किन्तु इसका सामान्यीकरण करते हुए किसी भी बन्द वक्र के किनारों की कुल लम्बाई को ‘परिधि’ कहा जाता हैं।

अर्थात परिधि, परिमाप की एक विशिष्ट अवस्था है। तीन या अधिक सरल रेखाओं से घिरे किसी बहुभुज की सभी भुजाओं की लम्बाई का योग परिमाप कहलाता हैं।

किसी ‘कोणरहित’ बन्द वक्र के बाहरी घेरे की कुल लम्बाई परिधि कहलाती हैं। परिधि ज्यामितीय और त्रिकोणमितीय अवधाराणओं में महत्वपूर्ण हैं।

किसी वृत्त की परिधि गणित में सभी गणितीय नियतांकों में से सबसे महत्वपूर्ण एक को सम्बद्ध करता है।

पाई, ग्रीक अक्षर पाई (π) से निरुपित किया जाता है।

π का संख्यात्मक मान 3.14159 26535 89793 … है और यह परिधि और व्यास के अनुपात के बराबर होता है।

Note :-

• जब वृत्त की त्रिज्या 1 हो तो उसकी परिधि 2π होती हैं।
• जब वृत्त का व्यास 1 हो तो उसकी परिधि π होती हैं।

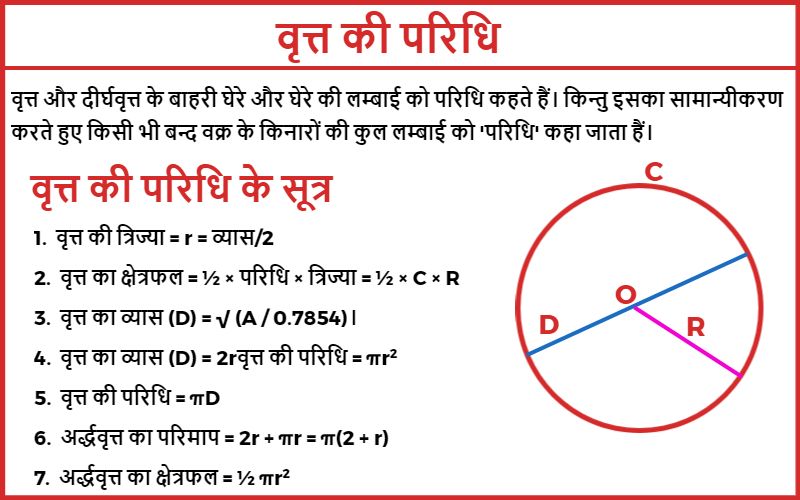
वृत्त की परिधि के सूत्र

• वृत्त की त्रिज्या = r = व्यास/2
• वृत्त का क्षेत्रफल = ½ × परिधि × त्रिज्या = ½ × C × R
• वृत्त का व्यास (D) = √(A / 0.7854)।
• वृत्त का व्यास (D) = 2r वृत्त की परिधि = πr²
• C = 2πr
• वृत्त की परिधि = πD
• अर्द्धवृत्त का परिमाप = 2r + πr = π(2 + r)
• अर्द्धवृत्त का क्षेत्रफल = ½ πr²

वृत्त की परिधि पर आधारित सवाल

Q.1 उस वृत्त की परिधि क्या होगी जिसकी त्रिज्या 21 सेंटीमीटर हैं?
A. 132 सेंटीमीटर
B. 146 सेंटीमीटर
C. 154 सेंटीमीटर
D. 172 सेंटीमीटर

हल:- प्रश्नानुसार,
C = 2πr
= 2 × 22/7 × 21
= 2 × 22 × 3
= 22 × 6
= 132
Ans. 132 सेंटीमीटर

Q.2 किसी रस्सी की लंबाई मीटर में कितनी होगी जिससे एक भैंस को बांधने पर वह 9856 वर्ग मीटर क्षेत्रफल को चर सके?
A. 56
B. 64
C. 88
D. 168

हल:- प्रश्नानुसार,
यदि रस्सी की लंबाई = r मीटर हैं तो
πr² = 9856
22/7 r² = 9856
r² = 9856 × 7/22
r² = 448 × 7
r² = 3136
r = √3136
r = 56 मीटर
Ans. 56 मीटर

Q.3 एक वन की परिधि 352 सेंटीमीटर हैं। इसका क्षेत्रफल क्या होगा?
A. 9856 वर्ग मीटर
B. 8956 वर्ग मीटर
C. 6589 वर्ग मीटर
D. 5986 वर्ग मीटर

हल:- प्रश्नानुसार,
C = 2πr
352 = 2πr
352 = 2 × 22/7 × r
r = 352 × 7/(2 × 22)
r = 176/22 × 7
r = 56 सेंटीमीटर
क्षेत्रफल = πr²
= 22/7 × 56 × 56
= 9856
Ans. 9856 वर्ग सेंटीमीटर

Q.4 56 सेंटीमीटर व्यास वाले अर्द्धवृत्त का परिमाप क्या होगा?
A. 144 सेंटीमीटर
B. 154 सेंटीमीटर
C. 166 सेंटीमीटर
D. 232 सेंटीमीटर

हल:- प्रश्नानुसार,
πr = 22/7 × 28
= 22 × 4
= 88 सेंटीमीटर
अर्द्ध वृत्त का परिमाप = 88 + 56
= 144 सेंटीमीटर
Ans. 144 सेंटीमीटर

Q.5 एक अर्द्ध-गोलाकार खिड़की जिसका व्यास 63 सेंटीमीटर हैं इसकी परिधि क्या होगी?
A. 126 सेंटीमीटर
B. 162 सेंटीमीटर
C. 198 सेंटीमीटर
D. 2161 सेंटीमीटर

हल:- प्रश्नानुसार,
r = 63/2
गोलाकार खिड़की की परिधि = πr + 2r
= 22/7 × 63/2 + 2 × 63/2
= 11 × 9 + 63
= 99 + 63
= 162
Ans. 162 सेंटीमीटर

FAQ

जरूर पढ़िए :
सांख्यिकी योग्यता	अंकगणित	कोष्ठक
भिन्न	दशमलव भिन्न	घातांक एवं करणी

उम्मीद हैं आपको परिधि की जानकारी पसंद आयी होगीं। यदि आपको यह जानकारी पसंद आयी हो तो इस पोस्ट को अपने दोस्तों के साथ जरूर शेयर करें धन्यवाद।