गोला की परिभाषा, गोले के सूत्र और उदाहरण

इस पेज पर आप गोला की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।

पिछले पेज पर हमने वृत्त की जानकारी शेयर की हैं तो उस पोस्ट को भी पढ़िए।

चलिए आज गोला की परिभाषा, गोले के सूत्र और उदाहरण की समस्त जानकारी को पढ़ते और समझते हैं।

गोला की परिभाषा

गोला वह ठोस हैं जिसमें केवल एक तल और एक आयाम होता हैं इसके तल का प्रत्येक बिन्दु एक निश्चित बिन्दु से समान दूरी पर होता हैं।

अर्थात गोला एक त्रिविमीय ठोस आकृति आकाश में स्थिर उन सभी बिन्दुओं से मिल कर बना है जो एक निश्चित बिंदु से एक अचर या निश्चित दूरी पर होते है वह गोला कहलाता हैं।

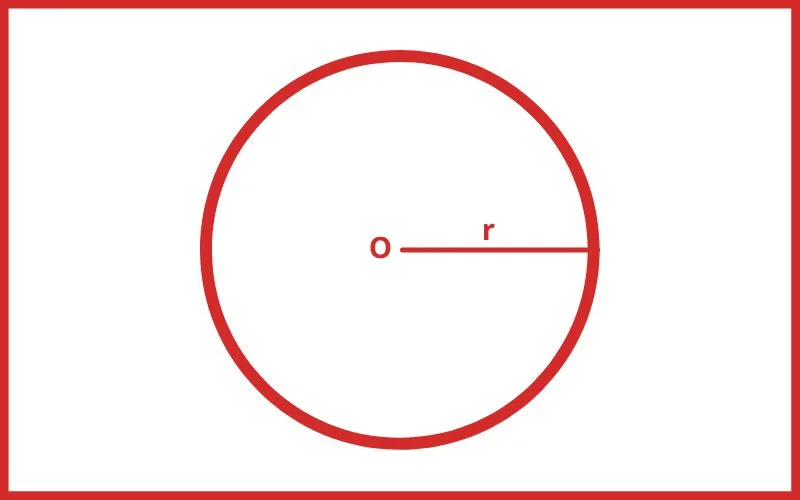
इस बिन्दु को गोले का केन्द्र कहते हैं तथा केन्द्र से गोले के किसी बिन्दु की दूरी को गोले की त्रिज्या कहते हैं।

दूसरे शब्दों में गोला एक ठोस आकृति है जो एक वृत्ताकार परत को इसके किसी भी व्यास के अनुदिश घुमाने से प्राप्त होता है वह गोला कहलाता हैं।

गोला के सूत्र

• गोले के वक्रपृष्ठ का क्षेत्रफल = 4πr² वर्ग सेंटीमीटर
• गोला का आयतन = 4/3 πr³ घन सेंटीमीटर
• गोलीय शेल का आयतन = ⁴⁄₃ π(R³ – r³)
• गोलीय शेल के सम्पूर्ण पृष्ठ का क्षेत्रफल = ⁴⁄₃ π(R²– r²)
• घन ने सबसे बड़े गोले का आयतन = ¹⁄₆ a³
• प्रत्येक घन में सबसे बड़े गोले की त्रिज्या = a/2
• घन में सबसे बड़े गोले का पृष्ठ क्षेत्रफल = πa²
• गोले में सबसे बड़े घन की एक भुजा = 2R / √3
• गोला में सबसे बड़े घन का आयतन = 8√3/a × R³
• गोला में सबसे बड़े घन का पृष्ठ क्षेत्रफल = 8 r²
  जहाँ a घन की भुजा तथा r गोले की त्रिज्या है।

अर्द्धगोले की परिभाषा

अर्द्ध गोला एक ऐसी त्रिआयामी ठोस आकृति है जिसे व्यास के अनुदिश दो बराबर भागो में बाँटने पर प्राप्त प्रत्येक भाग अर्द्धगोला कहलाता हैं।

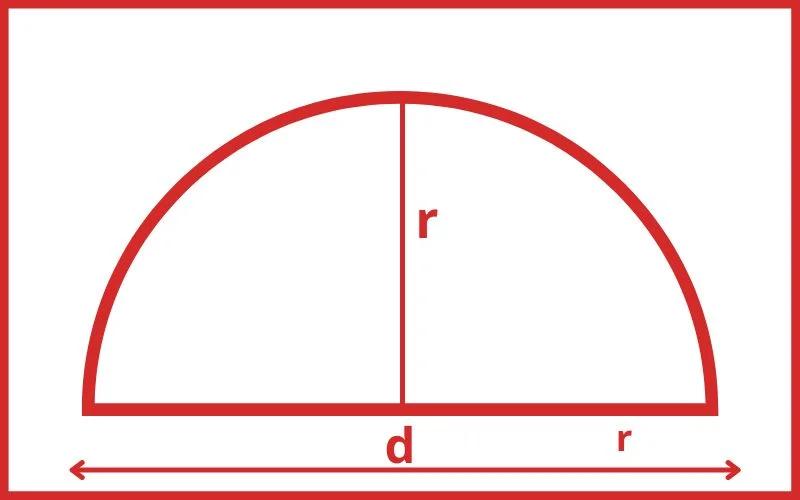
दूसरे शब्दों में एक ठोस गोले को बीचों बीच इसके केंद्र से जाते हुए एक तल के द्वारा दो समान भागों में काटें तो यह दो भागों में बंट जाता है प्रत्येक आधे भाग को अर्द्ध गोला कहते हैं।

किसी भी अर्द्ध गोला में दो वृताकार समतल फलक और दो वक्रीय फलक होते हैं।

अर्द्धगोले के सूत्र

• अर्द्धगोले का आयतन = (2πr³)/3 घन सेंटीमीटर
• अर्द्ध गोला के वक्रपृष्ठ का क्षेत्रफल = 2 πr²
• अर्द्धगोले का सम्पूर्ण पृष्ठ = 3πr² वर्ग सेंटीमीटर

अर्द्वगोले की त्रिज्या r हो, तो

• अर्द्वगोले का आयतन = 2/3 πr³
• अर्द्वगोले का वर्कप्रष्ठ = 2πr²
• अर्द्वगोले का सम्पूर्ण पृष्ठ = 3πr²

गोला एवं अर्द्ध गोला से सम्बंधित सूत्र

1. किसी गोले की त्रिज्या m गुनी करने पर क्षेत्रफल m² तथा आयतन m³ गुनी हो जाती है

2. गोला की त्रिज्या में x % की वृद्धि की जाए, तो क्षेत्रफल में (2x + x²/100) की वृद्धि होती हैं।

3. यदि गोला की त्रिज्या में x % की कमी की जाए, तो क्षेत्रफल में (2x – x²/100) की कमी होती हैं।

4. गोला की त्रिज्या में x % की वृद्धि की जाए, तो आयतन में [3x + 3x²/100 + x³/(100)³] की वृद्धि होती हैं।

5. यदि गोला की त्रिज्या में x % की कमी की जाए, तो आयतन में (3x + 3x²/(100)² – 3x²/100)की कमी होती हैं

6. अर्द्धगोलीय शेल का आयतन = 2/3 π(R³ – r³)

गोले के सवाल

Q.1 दो गोलों की त्रिज्याओं का अनुपात 1 : 2 हैं। उनके प्रष्ठ क्षेत्र फलों का अनुपात क्या होगा?
A. 1 : 2
B. 1 : 8
C. 1 : √2
D. 3 : 8

हल:- प्रश्नानुसार,
माना गोले की त्रिज्याएँ r तथा 2r हैं।
प्रष्ठ क्षेत्रफलों का अनुपात = 4 πr²/4π (2r)²
= 1/4
= 1 : 4
Ans. 1 : 4

Q.2 दो गोलों की त्रिज्याओं में 1 : 4 का अनुपात हैं। उनके प्रष्ठ क्षेत्रफलों में अनुपात होगा?
A. 1 : 4
B. 1 : 8
C. 1 : 12
D. 1 : 16

हल:- प्रश्नानुसार,
गोले के प्रष्ठ क्षेत्रफल में अनुपात = 4π(1)²/4π(4)²
= 1 : 16
Ans. 1 : 16

Q.3 यदि दो गोले के धरातल में 9 : 16 का अनुपात हैं तो उनके आयतनों में क्या अनुपात होगा?
A. 3 : 4
B. 9 : 16
C. 27 : 64
D. 81 : 256

हल:- प्रश्नानुसार,
माना गोलों की त्रिज्याएँ r₁² तथा r₂² हैं।
πr₁²/4πr₂² = 9/16
r₁²/r₂² = 9/16
r₁/r₂ = ³⁄₄
4/3 πr₁³ = 4/3 πr₂³
= r₁³ : r₂³
= 3³ : 4³
27 : 64
Ans. 27 : 64

Q.4 यदि गोले के प्रष्ठ क्षेत्रफल 4 : 25 के अनुपात में हो, तो उनके आयतनों का अनुपात होगा?
A. 4 : 25
B. 25 : 4
C. 125 : 4
D. 8 : 125

हल:- प्रश्नानुसार,
यदि गोले की त्रिज्याएँ क्रमशः r₁ तथा r₂ हो तो
4πr₁² : 4πr₂²
4 : 25
r₁ : r₂
2 : 5
4/3 πr₁³ : 4/3 πr₂³
8 : 125
Ans. 8 : 125

Q.5 एक गोले तथा घन के प्रष्ठ क्षेत्रफल बराबर हैं। गोले के आयतन का घन के आयतन से अनुपात होगा?
A. √π : √6
B. √2 : √π
C. √π : √3
D. √6 : √π

हल:- प्रश्नानुसार,
माना गोले की त्रिज्या r तथा घन की भुजा a हैं।
4πr³ = 6a²
a² = 4πr²/6
a = √2π/3 r
⁴⁄₃ πr³ : a³
⁴⁄₃ πr³ : (²⁄₃ π)³/2 r³
= ⁴⁄₃ π : 2√2 π³/²⁄₃√3
= √6 : √π
Ans. √6 : √π

जरूर पढ़िए :
घन	शंकु	बहुभुज
घनाभ	बेलन	आयतन

उम्मीद हैं आपको गोला की पोस्ट पसंद आयी होगीं।

यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ शेयर कीजिये।