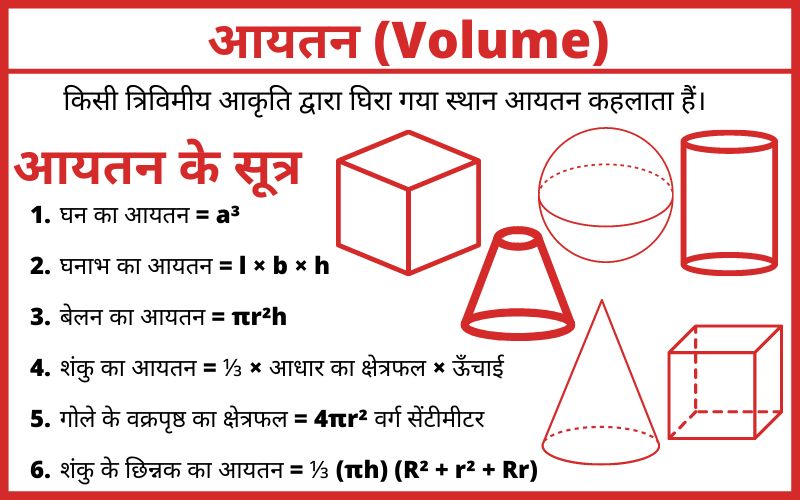
इस पेज पर आप आयतन की जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।
पिछले पेज पर हमने आयत और वर्ग की जानकारी शेयर की हैं तो उस पोस्ट को भी पढ़े।
चलिए अब हम आयतन की परिभाषा, आयतन का फार्मूला और उदाहरण की समस्त जानकारी को पढ़ते और समझते हैं।
Table of Contents
आयतन की परिभाषा
जो वस्तु जितनी जगह घेरती है उसे उस वस्तु का आयतन कहते हैं। किसी वस्तु का आयतन ज्ञात करने के लिए उस वस्तु की लम्बाई, चौड़ाई तथा उँचाई ज्ञात होना आवश्यक हैं।
किसी त्रिविमीय आकृति द्वारा घिरा गया स्थान आयतन कहलाता हैं। किसी पदार्थ द्वारा घिरे हुए स्थान की लम्बाई, चौड़ाई एवं ऊँचाई में व्यक्त किया जाता हैं। आयतन को हमेशा घन इकाई में मापा जाता हैं।
S.I. पद्धति में आयतन का मात्रक मीटर³ होता हैं।
त्रिविमीय आकृतियों के अंतगर्त घन, घनाभ, बेलन, शंकु, गोला, शंकु का छिन्नक आदि आते हैं।
घन क्या हैं
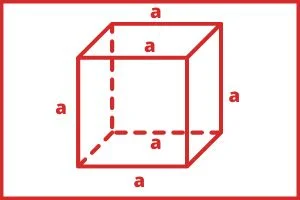
घन की लम्बाई, चौड़ाई एवं ऊँचाई सामान होती हैं। एक घन में छः फलक, बारह किनारे एवं आठ कोने होते हैं इसके छह बराबर-बराबर आकार के फलक होते हैं हर फलक एक वर्ग होता हैं और छह फलक होने के कारण यह एक प्रकार का षट्फलकी भी कहलाता हैं।
घन के सूत्र
- घन का आयतन = a × a × a
- घन का परिमाप = 4 × a × a
- घन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 6 a² वर्ग सेंटीमीटर।
- घन का विकर्ण = √3a सेंटीमीटर।
घनाभ क्या हैं
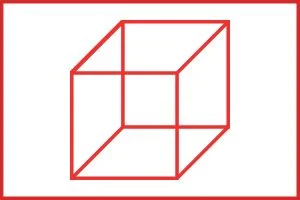
छः पृष्ठों से घिरी वह आकृति, जिसमें प्रत्येक पृष्ठ एक आयत होता हैं और सम्मुख पृष्ठ बराबर होते हैं घनाभ कहलाता हैं।
जैसे :- किताब, ईट, दियासलाई की डिबिया संदूक इत्यादि।
घनाभ के सूत्र
- घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई
- घनाभ का आयतन = l × b × h
- घनाभ का परिमाप = 2(l + b) × h
- घनाभ के समस्त पृष्ठों का क्षेत्रफल = 2(लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई)
- घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl)
- घनाभ के विकर्ण = √(लम्बाई)² + (चौड़ाई)² + (ऊँचाई)²
- घनाभ का विकर्ण = √l² + b² + h²
बेलन क्या हैं
बेलन ज्यामिति में एक त्रिआयामी ठोस की आकृति है। इसका पार्श्व पृष्ठ वक्र, सिरे समान त्रिज्या के वृत्ताकार होते हैं, बेलन सरल रूप में एक रोलर या समान व्यास का गिलास है।
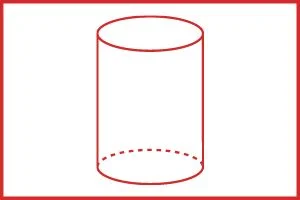
किसी वृत्त की परिधि पर लम्ब रूप से हमेशा अपने ही समांतर किसी सरल रेखा के घूमने से जिस पिण्ड का निर्माण होता हैं उसे बेलन कहते हैं।
बेलन के सूत्र
- बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई
= πr²h - बेलन का वक्रप्रष्ठ = आधार की परिमाप × ऊँचाई = 2πrh
- बेलन का सम्पूर्ण प्रष्ठ = वक्रप्रष्ठ का क्षेत्रफल + 2 × आधार का क्षेत्रफल = 2πrh + 2πr²
= 2πr(r + h) - खोखले बेलन का आयतन = πh(r₁² – r₂²)
- खोखले बेलन का वक्रप्रष्ठ = 2πh(r₁² + r₂²)
- खोखले बेलन का सम्पूर्ण प्रष्ठ = 2πh(r₁ + r₂) + 2π(r₁² – 2r₂²)
शंकु क्या हैं
कोई समकोण त्रिभुज अपने स्थिर लम्ब के चारों ओर घूमकर जिस पिण्ड का निर्माण करता हैं उसे लम्बवृत्तीय शंकु कहते हैं।
दूसरे शब्दों में, शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं यदि किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।
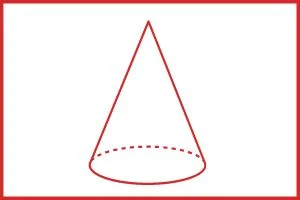
AC या AE को तिर्यक ऊँचाई तथा CAE को शीर्ष तथा कोण BAC को अर्द्ध शीर्ष कोण कहते हैं।
माना, आधार की त्रिज्या r, ऊँचाई h तथा तिर्यक ऊँचाई हो, तो
शंकु के सूत्र
- शंकु का आयतन = ⅓ × आधार का क्षेत्रफल × ऊँचाई
= ⅓ π²h - शंकु का वक्रतल = ½ × आधार की परिधि × तिर्यक ऊँचाई
= πrl - शंकु का सम्पूर्ण सतह = वक्रप्रष्ठ + आधार का क्षेत्रफल = πr (l + r)
- शंकु की तिर्यक ऊँचाई = √(त्रिज्या)² + (ऊँचाई)²
L = √r² + h²
गोला की परिभाषा
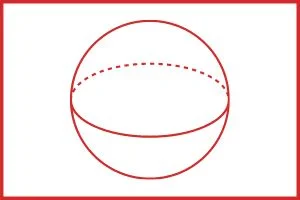
गोला वह ठोस हैं जिसमें केवल एक तल और एक आयाम होता हैं इसके तल का प्रत्येक बिन्दु एक निश्चित बिन्दु से समान दूरी पर होता हैं।
अर्थात गोला एक त्रिविमीय ठोस आकृति आकाश में स्थिर उन सभी बिन्दुओं से मिल कर बना है जो एक निश्चित बिंदु से एक अचर या निश्चित दूरी पर होते है वह गोला कहलाता हैं।
गोला के सूत्र
- गोले के वक्रपृष्ठ का क्षेत्रफल = 4πr² वर्ग सेंटीमीटर
- गोला का आयतन = 4/3 πr³ घन सेंटीमीटर
- गोलीय शेल का आयतन = ⁴⁄₃ π(R³ – r³)
- गोलीय शेल के सम्पूर्ण पृष्ठ का क्षेत्रफल = ⁴⁄₃ π(R²– r²)
- घन ने सबसे बड़े गोले का आयतन = ¹⁄₆ a³
- प्रत्येक घन में सबसे बड़े गोले की त्रिज्या = a/2
- घन में सबसे बड़े गोले का पृष्ठ क्षेत्रफल = πa²
- गोले में सबसे बड़े घन की एक भुजा = 2R / √3
- गोला में सबसे बड़े घन का आयतन = 8√3/a × R³
- गोला में सबसे बड़े घन का पृष्ठ क्षेत्रफल = 8 r²
शंकु का छिन्नक किसे कहते हैं
शंकु के कुछ उपरी भाग को आधार के समान्तर समतल द्वारा काट देने पर बचे ठोस को शंकु का छिन्नक कहते हैं।
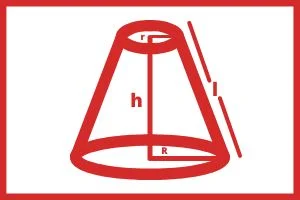
शंकु का ऊपरी भाग आकार में समान रहता है लेकिन नीचे का भाग एक छिन्नक बनाता हैं। यह एक प्रकार का ग्लासनुमा आकृति होता हैं। जो शंकु के दो बराबर भाग में काटने पर प्राप्त होता हैं।
शंकु का छिन्नक के सूत्र
- शंकु के छिन्नक का आयतन = ⅓ (πh) (R² + r² + Rr)
- छिन्नक का वक्र पृष्ठ का क्षेत्रफल = πL(R + r)
- तिर्यक भाग का क्षेत्रफल = π (R + r)³, l² = h² + (R – r)²
- छिन्नक के सम्पूर्ण पृष्ठ का क्षेत्रफल = π[R² + r² + l(R + r)]
आयतन के सूत्र
- घन का आयतन = a × a × a
- घन का परिमाप = 4 × a × a
- घन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 6 a² वर्ग सेंटीमीटर।
- घन का विकर्ण = √3a सेंटीमीटर।
- घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई
- घनाभ का आयतन = l × b × h
- घनाभ का परिमाप = 2(l + b) × h
- घनाभ के समस्त पृष्ठों का क्षेत्रफल = 2(लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई)
- घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl)
- घनाभ के विकर्ण = √(लम्बाई)² + (चौड़ाई)² + (ऊँचाई)²
- घनाभ का विकर्ण = √l² + b² + h²
- बेलन का आयतन = πr²h
- बेलन का वक्रप्रष्ठ = आधार की परिमाप × ऊँचाई = 2πrh
- बेलन का सम्पूर्ण प्रष्ठ = 2πr(r + h)
- खोखले बेलन का आयतन = πh(r₁² – r₂²)
- खोखले बेलन का वक्रप्रष्ठ = 2πh(r₁² + r₂²)
- खोखले बेलन का सम्पूर्ण प्रष्ठ = 2πh(r₁ + r₂) + 2π(r₁² – 2r₂²)
- शंकु का आयतन = ⅓ × आधार का क्षेत्रफल × ऊँचाई
- शंकु का वक्रतल = ½ × आधार की परिधि × तिर्यक ऊँचाई
- शंकु का सम्पूर्ण सतह = वक्रप्रष्ठ + आधार का क्षेत्रफल = πr (l + r)
- शंकु की तिर्यक ऊँचाई L = √r² + h²
- गोले के वक्रपृष्ठ का क्षेत्रफल = 4π r² वर्ग सेंटीमीटर
- गोला का आयतन = 4/3 π r³ घन सेंटीमीटर
- गोलीय शेल का आयतन = ⁴⁄₃ π(R³ – r³)
- गोलीय शेल के सम्पूर्ण पृष्ठ का क्षेत्रफल = ⁴⁄₃ π(R²– r²)
- घन ने सबसे बड़े गोले का आयतन = ¹⁄₆ a³
- प्रत्येक घन में सबसे बड़े गोले की त्रिज्या = a/2
- घन में सबसे बड़े गोले का पृष्ठ क्षेत्रफल = πa²
- गोले में सबसे बड़े घन की एक भुजा = 2R / √3
- गोला में सबसे बड़े घन का आयतन = 8√3/a × R³
- गोला में सबसे बड़े घन का पृष्ठ क्षेत्रफल = 8 r²
- शंकु के छिन्नक का आयतन = ⅓ (π h) (R² + r² + Rr)
- छिन्नक का वक्र पृष्ठ का क्षेत्रफल = πL(R + r)
- तिर्यक भाग का क्षेत्रफल = π (R + r)³, l² = h² + (R – r)²
- छिन्नक के सम्पूर्ण पृष्ठ का क्षेत्रफल = π [R² + r² + l(R + r)]
आयतन के सवाल
Q.1 एक घन का प्रत्येक किनारा 5 मीटर हैं, तो उसका कुल पृष्ठ क्षेत्रफल और आयत होगा?
A. 150 वर्ग मीटर, 125 घन मीटर
B. 25 वर्ग मीटर, 75 घन मीटर
C. 190 वर्ग मीटर, 175 घन मीटर
D. 40 वर्ग मीटर, 160 घन मीटर
हल:- प्रश्ननानुसार,
घन का कुल प्रष्ठ क्षेत्रफल = 6 × (भुजा)²
= 6 × 25
= 150 वर्ग मीटर
घन का आयतन = (भुजा)²
= (5)²
= 25
Ans. 25 घन मीटर
Q.2 एक घनाभ की लम्बाई 15 मीटर, चौड़ाई 10 मीटर तथा ऊँचाई 4 मीटर हैं। इसका सम्पूर्ण प्रष्ठ हैं?
A. 420 वर्ग मी.
B. 450 वर्ग मी.
C. 500 वर्ग मी.
D. 600 वर्ग मी.
हल:- प्रश्ननानुसार,
घनाभ का सम्पूर्ण प्रष्ठ = 2(15 × 10 + 10 × 4 + 4 × 15)
= 500 वर्ग मीटर
उत्तर:- 500 वर्ग मीटर
Q.3 यदि गोले के प्रष्ठ क्षेत्रफल 4 : 25 के अनुपात में हो, तो उनके आयतनों का अनुपात होगा?
A. 4 : 25
B. 25 : 4
C. 125 : 4
D. 8 : 125
हल:- प्रश्नानुसार,
यदि गोले की त्रिज्याएँ क्रमशः r₁ तथा r₂ हो तो
4πr₁² : 4πr₂²
4 : 25
r₁ : r₂
2 : 5
4/3 πr₁³ : 4/3 πr₂³
8 : 125
Ans. 8 : 125
Q.4 यदि गोले के प्रष्ठ क्षेत्रफल 4 : 25 के अनुपात में हो, तो उनके आयतनों का अनुपात होगा?
A. 4 : 25
B. 25 : 4
C. 125 : 4
D. 8 : 125
हल:- प्रश्नानुसार,
यदि गोले की त्रिज्याएँ क्रमशः r₁ तथा r₂ हो तो
4πr₁² : 4πr₂²
4 : 25
r₁ : r₂
2 : 5
⁴⁄₃ πr₁³ : 4/3 πr₂³
8 : 125
Ans. 8 : 125
Q.5 एक गोले तथा घन के प्रष्ठ क्षेत्रफल बराबर हैं। गोले के आयतन का घन के आयतन से अनुपात होगा?
A. √π : √6
B. √2 : √π
C. √π : √3
D. √6 : √π
हल:- प्रश्नानुसार,
माना गोले की त्रिज्या r तथा घन की भुजा a हैं।
4πr³ = 6a²
a² = 4πr²/6
a = √2π/3 r
⁴⁄₃ πr³ : a³
⁴⁄₃ πr³ : (2/3 π)³/2 r³
= 4/3 π : 2√2 π³/2/3√3
= √6 : √π
Ans. √6 : √π
Q.6 70 सेंटीमीटर आधार त्रिज्या और 40040 सेंटीमीटर के वक्रपृष्ठ क्षेत्र वाले लम्ब वृत्तीय शंकु का आयतन होगा?
A. 862400 सेंटीमीटर³
B. 863200 सेंटीमीटर³
C. 862200 सेंटीमीटर³
D. 865800 सेंटीमीटर³
हल:- प्रश्नानुसार,
शंकु का वक्रप्रष्ठ = πrl
= 40040
l = 182 सेंटीमीटर
h² = l² – t²
h² = (182)² – (70)²
h² = 28224
h = 168
शंकु का आयतन = ⅓ πr²h
= ⅓ × 22/7 × (70)² × 168
= 862400 सेंटीमीटर
Ans. 862400 सेंटीमीटर³
Q.7 एक बेलन का वक्रप्रष्ठ 264 वर्ग मीटर हैं। उसका आयतन 924 घन मीटर हैं। तो बेलन की ऊँचाई हैं?
A. 4 मीटर
B. 6 मीटर
C. 8 मीटर
D. 10 मीटर
हल:- बेलन का वक्रप्रष्ठ = 2πrh
प्रश्नानुसार,
264 = 2 × 22/7 × rh
rh = 42
πr²h = 924
r = 7
h = 6 मीटर
Ans. 6 मीटर
Q.8 2.5 मिलीमीटर मोटे और बाहरी व्यास 20 सेंटीमीटर लम्बाई 16 सेंटीमीटर के खोखले बेलन को ढालने के लिए 2 सेंटीमीटर व्यास के ठोस बेलन की लंबाई क्या होनी चाहिए?
A. 81 सेंटीमीटर
B. 29.62 सेंटीमीटर
C. 39.5 सेंटीमीटर
D. 79 सेंटीमीटर
हल:- माना, कि ठोस बेलन की ऊँचाई h सेंटीमीटर हैं।
प्रश्नानुसार,
π × (²⁄₂)² × h
π × {(²⁰⁄₂)² – (¹⁹⋅⁵)²⁄₂} × 16
h = {100 – 95.0625} × 16
= 4.9375 × 16
= 79
Ans. 79 सेंटीमीटर
Q.9 2 सेंटीमीटर भुजा के लकड़ी का एक घन हैं। यदि इसमें अधिकतम आयतन का बेलन काटा जाए तो शेष बची हुई लकड़ी का आयतन कितना होगा?
A. 9/7 घन सेंटीमीटर
B. 10/7 घन सेंटीमीटर
C. 11/7 घन सेंटीमीटर
D. 12/7 घन सेंटीमीटर
हल:- प्रश्नानुसार,
बेलन की ऊँचाई = 2 सेंटीमीटर
त्रिज्या = 1 सेंटीमीटर
घन का आयतन = 2³
= 8 घन सेंटीमीटर
बेलन का आयतन = 22/7 × 1 × 1 × 2
= 44/7 घन सेंटीमीटर
शेष लकड़ी का आयतन = 8 – 44/7
= (56 – 44)/7
= 12/7 घन सेंटीमीटर
Ans. 12/7 घन सेंटीमीटर
Q.10 दो बेलनों के आधारों की त्रिज्याओं का अनुपात 2 : 3 हैं तथा उनकी ऊंचाइयों का अनुपात 5 : 3 हैं। इनके आयतनों का अनुपात क्या होगा?
A. 27 : 20
B. 20 : 27
C. 4 : 9
D. 9 : 4
हल:- माना, बेलनों की त्रिज्याएँ क्रमशः 2r तथा 3r हैं।
ऊँचाई 5h तथा 3h हैं।
आयतनों का अनुपात = π(2r)² × 5h/π(3r)² × 3h
= 20 : 27
Ans. 20 : 27
उम्मीद हैं आपको आयतन की यह आर्टिकल पसंद आयी होगी।
यदि आपको आयतन की पोस्ट पसंद आयी हो तो दोस्तों के साथ शेयर कीजिए।
आयतन से सम्बंधित किसी भी प्रश्न के लिए कमेंट करें।