इस पेज पर आप त्रिभुज की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।
पिछले पेज पर हमने साधारण ब्याज और चक्रवृद्धि ब्याज की जानकारी शेयर की हैं उन आर्टिकल्स को भी पढ़े।
चलिए आज हम त्रिभुज की जानकारी को पढ़ते और समझते हैं।
Table of Contents
त्रिभुज क्या हैं
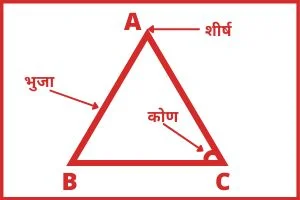
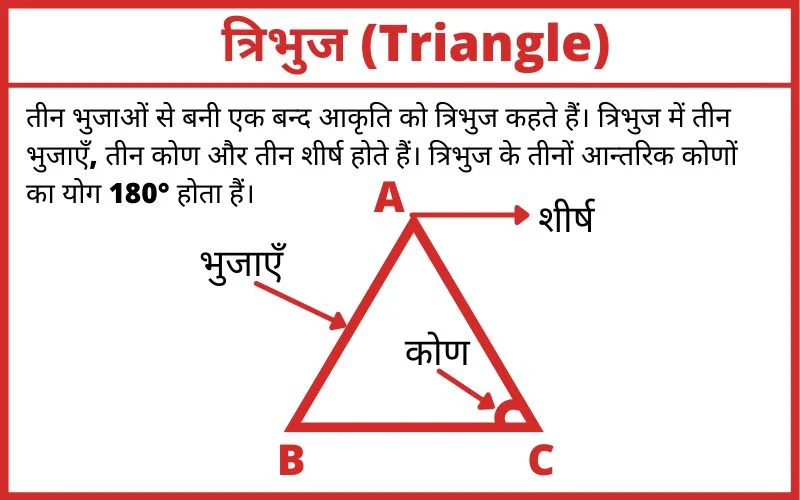
तीन भुजाओं से बनी एक बन्द आकृति को त्रिभुज कहते हैं। त्रिभुज में तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। त्रिभुज सबसे कम भुजाओं वाला एक बहुभुज हैं। त्रिभुज के तीनों आन्तरिक कोणों का योग 180° होता हैं।
त्रिभुज की भुजाओं को A, B, और C के नामों से प्रदर्शित किया जाता हैं। तथा कोणों को ∠A, ∠B, और ∠C द्वारा प्रदर्शित किया जाता हैं।
त्रिभुज का सूत्र
त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
त्रिभुज के प्रकार
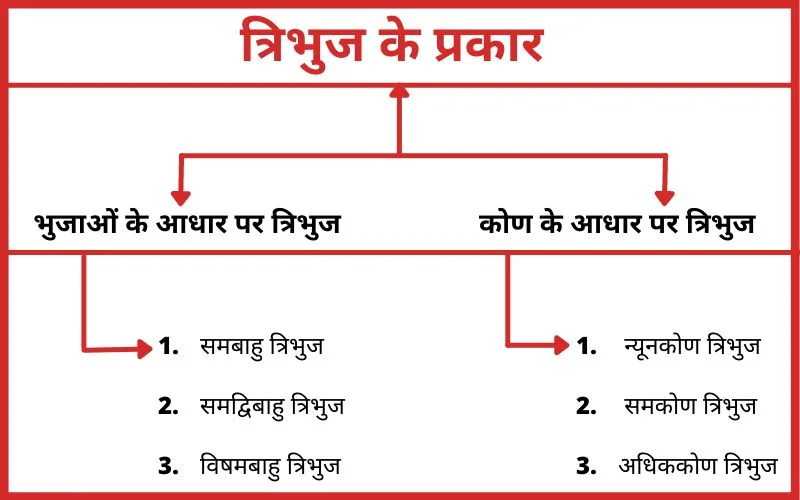
भुजाओं और कोण के आधार पर त्रिभुज दो प्रकार के होते हैं।
- भुजाओं के आधार पर त्रिभुज
- कोण के आधार पर त्रिभुज
1. भुजाओं के आधार पर त्रिभुज
भुजाओं के आधार पर त्रिभुज 3 प्रकार के होते हैं। त्रिभुज का परिमाप हमेशा उसकी तीनों भुजाओं का योग होता है।
(a). समबाहु त्रिभुज
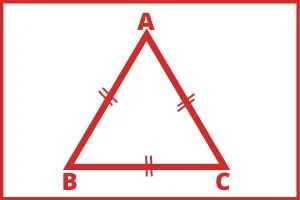
जिस त्रिभुज की सभी भुजाएं आपस में बराबर होती हैं उसे समबाहु त्रिभुज कहते हैं। समबाहु त्रिभुज के प्रत्येक कोण का मान 60° होता हैं।
समबाहु त्रिभुज के सूत्र
- समबाहु त्रिभुज का क्षेत्रफल = √3/4 × भुजा²
- समबाहु त्रिभुज का परिमाप = 3 × भुजा
- शीर्ष बिंदु से डाले गए लम्ब की लम्बाई = √3/4 × भुजा
- समबाहु त्रिभुज के अर्धवृत की त्रिज्या R = a/2 × √3
- परिवृत की त्रिज्या R = a/√3
(b). समद्विबाहु त्रिभुज
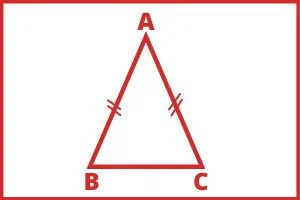
ऐसा त्रिभुज जिसकी तीन भुजाओं में से कोई दो भुजाएं समान होती हो समद्विबाहु त्रिभुज कहलाता हैं।
समद्विबाहु त्रिभुज के सूत्र
- समद्विबाहु त्रिभुज का क्षेत्रफल A = ½ × आधार × ऊँचाई
क्षेत्रफल A = ½ × b × h - दूसरा क्षेत्रफल A = a/4 √(4b² – a²)
- तीसरा क्षेत्रफल A = ½ × side2 × sinθ
- समद्विबाहु त्रिभुज का परिमाप P = 2a + b
(c). विषमबाहु त्रिभुज
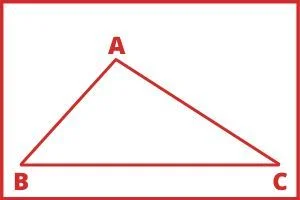
जिस त्रिभुज की तीनों भुजाएँ अलग-अलग लम्बाई की हों उसे विषमबाहु त्रिभुज कहते हैं। इस त्रिभुज की तीनों भुजाएं अलग-अलग माप की होती हैं।
विषमबाहु त्रिभुज के सूत्र
- विषमबाहु त्रिभुज का क्षेत्रफल A = ½ × b × h
- A = ½ × आधार × ऊँचाई
- क्षेत्रफल A = ½ × a × b × sinθ
- त्रिभुज का अर्धपरिधि P = ½ ( a + b + c )
- क्षेत्रफल A = √s(s – a)(s – b)(s – c)
2. कोण के आधार पर त्रिभुज
कोण के आधार पर त्रिभुज 3 प्रकार के होते हैं।
(a). न्यूनकोण त्रिभुज
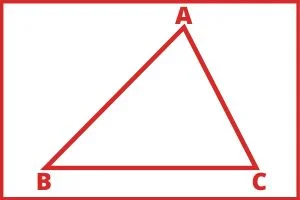
जिस त्रिभुज के प्रत्येक कोण का मान 90 डिग्री से कम होता है उसे न्यूनकोण त्रिभुज कहते हैं।
न्यूनकोण त्रिभुज की तीनों भुजाओं का योग 180 डिग्री के बराबर होता हैं।
न्यूनकोण त्रिभुज के सूत्र
- न्यूनकोण त्रिभुज का क्षेत्रफल A = ½ × b × h
- न्यूनकोण त्रिभुज का परिमाप = a + b + c
- क्षेत्रफल A = √s(s – a)(s – b)(s – c)
- A = ½ × a × b × sinθ
- न्यूनकोण त्रिभुज का क्षेत्रफल A = ½ × b × h
(b). समकोण त्रिभुज
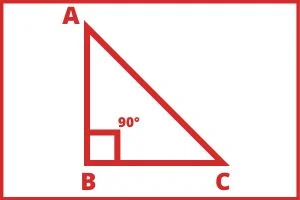
जिस त्रिभुज में एक कोण समकोण अर्थात 90° का हो उस त्रिभुज को समकोण त्रिभुज कहलाता हैं।
समकोण त्रिभुज के सूत्र
कर्ण की लम्बाई का वर्ग = लम्ब की लम्बाई का वर्ग + आधार की लम्बाई का वर्ग
AC² = AB² + BC²
- (कर्ण)² = (लम्ब)² + (आधार)²
- समकोण त्रिभुज का कर्ण = √लम्ब² +आधार²
- समकोण त्रिभुज का लम्ब = √कर्ण² – आधार²
- समकोण त्रिभुज का आधार = √कर्ण² – लम्ब²
- समकोण त्रिभुज का क्षेत्रफल A = ½ × आधार × ऊँचाई
- क्षेत्रफल = A = ½ × b × h
- कर्ण C = √a² + b²
- परिमाप = a + b + c
- ऊँचाई = (a × b)/c
(c). अधिककोण त्रिभुज
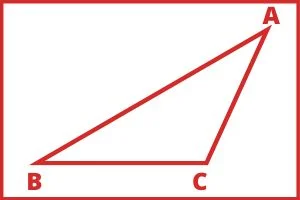
जिस त्रिभुज का एक कोण 90° से अधिक हो उस त्रिभुज को अधिककोण त्रिभुज कहते हैं। इस त्रिभुज के प्रत्येक आंतरिक कोणों का योग सदैव 180 डिग्री के बराबर होता हैं।
अधिककोण त्रिभुज के सूत्र
- क्षेत्रफल A = ½ × b × h
- परिमाप = a + b + c
- अर्धपरिधि P = ½ ( a + b + c )
- क्षेत्रफल A = √s(s – a)(s – b)(s – c)
त्रिभुजों की विशेषताएं
1. त्रिभुज के तीनों कोणों का मान 180° π रेडियन होता हैं।
2. त्रिभुज के तीन शीर्ष, तीन भुजाएँ और तीन कोण होता हैं।
3. त्रिभुज के दो भुजाओं का योग तीसरी भुजा से अधिक होती हैं।
4. त्रिभुज के दो भुजाओं का अंतर तीसरी भुजा से छोटी होती हैं।
5. त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से बड़ा होता हैं।
6. त्रिभुज की कोई दो भुजाओं की मापों का अंतर, तीसरी भुजा की माप से कम होता हैं।
7. यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो यह रेखा तीसरी भुजा के समांतर होती हैं।
8. त्रिभुज की एक भुजा को आगे बढ़ाने पर बनने वाला बहिष्कोण दो सम्मुख अन्त: कोणों के योग के बराबर होता हैं। त्रिभुज का बहिष्कोण किसी भी सम्मुख अन्त:कोण से बड़ा होता हैं।
9. यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करने के लिए, एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
10. यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में होती हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं।
11. यदि दो त्रिभुजों में, एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के बराबर हों, तो दोनों त्रिभुज
समरूप होते हैं।
12. यदि दो त्रिभुजों में, संगत भुजाएँ एक ही अनुपात में हों, तो उनके संगत कोण बराबर होते हैं और इसलिए दोनों त्रिभुज समरूप होते हैं।
13. यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में हों तो दोनों त्रिभुज समरूप होते हैं।
14. यदि एक त्रिभुज में किसी एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो पहली भुजा का
सम्मुख कोण समकोण होता हैं।
त्रिभुज के उदाहरण
Q.1 एक त्रिभुज का आधार 8 सेंटीमीटर तथा त्रिभुज की ऊंचाई 12 सेंटीमीटर हैं तो त्रिभुज का क्षेत्रफल बताइए?
A. 12 सेंटीमीटर
B. 24 सेंटीमीटर
C. 36 सेंटीमीटर
D. 48 सेंटीमीटर
हल:- प्रश्ननानुसार,
आधार = 8 सेंटीमीटर
ऊंचाई = 12 सेंटीमीटर
त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
= ½ × 8 × 12
= 4 × 12
= 48
Ans. 48 सेंटीमीटर
Q.2 एक त्रिभुज का आधार 14 सेंटीमीटर तथा त्रिभुज की ऊंचाई 20 सेंटीमीटर हैं तो त्रिभुज का क्षेत्रफल बताइए?
A. 120 सेंटीमीटर
B. 124 सेंटीमीटर
C. 136 सेंटीमीटर
D. 140 सेंटीमीटर
हल:- प्रश्ननानुसार,
आधार = 14 सेंटीमीटर
ऊंचाई = 20 सेंटीमीटर
त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
= ½ × 14 × 20
= 7 × 20
= 140
Ans. 140 सेंटीमीटर
Q.3 यदि किसी त्रिभुज का आधार दूना तथा ऊँचाई आधी कर दी जाए तो परिवर्तन से पूर्व तथा बाद के क्षेत्रफलों में क्या अनुपात होगा?
A. 3 : 2
B. 1 : 1
C. 2 : 1
D. 3 : 1
हल:- प्रश्ननानुसार,
त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
= ½ × x × y
नये त्रिभुज का क्षेत्रफल = ½ × 2x × y/2
= ½ xy
अभीष्ट अनुपात = xy/2/(xy/2)
= xy/2 × 2/xy
= 1 : 1
Ans. 1 : 1
Q.4 किसी त्रिभुज का परिमाप 30 सेंटीमीटर और उसका क्षेत्रफल 30 वर्ग सेंटीमीटर हैं। यदि त्रिभुज की सबसे बड़ी भुजा की लम्बाई 13 सेंटीमीटर हैं। तो उसकी सबसे छोटी भुजा की लम्बाई ज्ञात कीजिए?
A. 3 सेंटीमीटर
B. 4 सेंटीमीटर
C. 5 सेंटीमीटर
D. 6 सेंटीमीटर
हल:- प्रश्ननानुसार,
माना कि त्रिभुज की सबसे छोटी भुजा = x सेंटीमीटर
मध्य की भुजा = 30 – (13 + x)
= (17 – x) सेंटीमीटर
S = (a + b + c)/2
S = (17 + x + 17 – x)/2
S = 15 सेंटीमीटर
∆ का क्षेत्रफल = √s(s – a)(s – b)(s – c)
30 = √15(15 – 13)(15 – x)(15 – 17 + x)
30 = √30 (15 – x)(x – 2)
30 = √30 (15x – 30 – x² + 2x)
दोनों पक्षों का वर्ग करने पर,
(30)² = [√30 (15x – 30 – x² + 2x)]²
900 = 30(17x – x² – 30)
900/30 = (17x – x² – 30)
30 = 17x – x² – 30
30 + 30 = 17x – x²
60 = 17x – x²
x² – 17x + 60 = 0
x² – 12x – 5x + 60 = 0
x(x – 12) – 5(x – 12) = 0
(x – 12)(x – 5) = 0
x = 12
x = 5
अतः सबसे छोटी भुजा 5 होगीं।
Ans. 5 सेंटीमीटर
Q.5 किसी त्रिभुज का क्षेत्रफल 216 सेंटीमीटर² हैं और उसकी भुजाएँ 3 : 4 : 5 के अनुपात में हैं। इस त्रिभुज का परिमाप हैं?
A. 6 सेंटीमीटर
B. 12 सेंटीमीटर
C. 36 सेंटीमीटर
D. 72 सेंटीमीटर
हल:- प्रश्ननानुसार,
माना त्रिभुज की भुजाएँ 3x, 4x तथा 5x हैं।
(5x)² = (3x)² + (4x)²
त्रिभुज समकोण त्रिभुज हैं तब
½ + 3x × 4x = 216
x = 6
त्रिभुज का परिमाप = (3x + 4x + 5x) = 12x
= 12 × 6
= 72 सेंटीमीटर
Ans. 72 सेंटीमीटर
Q.6 एक त्रिभुज की भुजाएँ 5 : 4 : 3 के अनुपात में हैं। यदि त्रिभुज की परिमाप 24 सेंटीमीटर हैं तो त्रिभुज का क्षेत्रफल क्या होगा?
A. 12 वर्ग सेंटीमीटर
B. 24 वर्ग सेंटीमीटर
C. 6 वर्ग सेंटीमीटर
D. 47 वर्ग सेंटीमीटर
हल:-
माना त्रिभुज की भुजाएँ = 5x, 4x और 3x
प्रश्ननानुसार,
5x + 4x + 3x = 24
12x = 24
x = 2
भुजाएँ = 5x, 4x और 3x हैं।
5x = 5 × 2 = 10
4x = 4 × 2 = 8
3x = 3 × 2 = 6
S = (a + b + c)/2
S = (10 + 8 + 6)/2
S = 24/2
S = 12 सेंटीमीटर
∆ का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ का क्षेत्रफल = √12(12 – 10)(12 – 8)(12 – 6)
∆ का क्षेत्रफल = √12 × 2 × 4 × 6
∆ का क्षेत्रफल = 24
उत्तर:- 24 वर्ग सेंटीमीटर
जरूर पढ़िए :
उम्मीद हैं आपको त्रिभुज की जानकारी पसंद आयी होगीं।
यदि आपको त्रिभुज की जानकारी पसंद आयी हो तो दोस्तों के साथ शेयर करें।