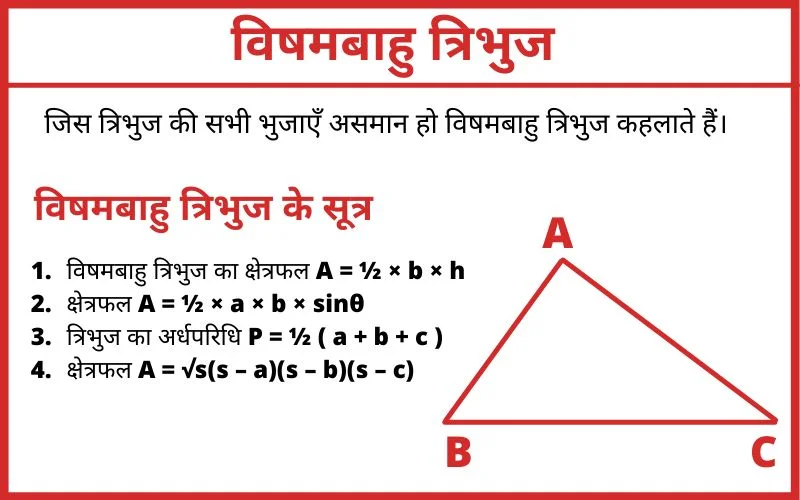
इस पेज पर आप गणित के महत्वपूर्ण अध्याय विषमबाहु त्रिभुज की जानकारी को पढ़ने वाले हैं।
पिछले पेज पर हमने समबाहु त्रिभुज की जानकारी शेयर की हैं तो उस पोस्ट को भी जरूर पढ़े।
चलिए इस पेज पर विषमबाहु त्रिभुज की समस्त जानकारी को पढ़ते और समझते हैं।
Table of Contents
विषमबाहु त्रिभुज की परिभाषा
जिस त्रिभुज की सभी भुजाएँ असमान हो उसे विषमबाहु त्रिभुज कहते हैं।
विषमबाहु त्रिभुज की तीनों भुजाएँ एवं कोण अलग-अलग लम्बाई एवं माप के होते हैं। लेकिन इस त्रिभुज में समरूपता की कोई रेखा नहीं होती हैं। इसके आंतरिक कोणों का योग सदैव 180 डिग्री के बराबर होता हैं।
विषमबाहु त्रिभुज के सूत्र
- विषमबाहु त्रिभुज का क्षेत्रफल A = ½ × b × h
A = ½ × आधार × ऊँचाई - क्षेत्रफल A = ½ × a × b × sinθ
जहाँ, a = ऊँचाई, b = आधार तथा θ = थीटा, (त्रिभुज का कोण)
हिरोंन का सूत्र
हीरोन का सूत्र विषमबाहु त्रिभुज की तीनों भुजाएँ ज्ञात होने के बाद उसका क्षेत्रफल निकालने के प्रयोग किया जाता हैं। सबसे पहले त्रिभुज का परिमाप ज्ञात किया जाता हैं। उसके बाद हीरोन सूत्र का प्रयोग किया जाता हैं।
हीरोन के इस सूत्र का नाम अलेक्जैण्ड्रिया के हीरोन के नाम पर पढ़ा था इसलिये इसे हीरो का सूत्र भी कहा जाता हैं।
यदि किसी त्रिभुज की तीन भुजाएँ a, b और c हों, तो
- त्रिभुज का अर्धपरिधि P = ½ ( a + b + c )
- क्षेत्रफल A = √s(s – a)(s – b)(s – c)
जहाँ a, b, और c त्रिभुज की भुजाएँ है तथा S त्रिभुज की अर्धपरिमाप हैं।
विषमबाहु त्रिभुज के गुण
- इस त्रिभुज में तीनों भुजाएं अलग अलग माप की होती हैं।
- इस त्रिभुज के तीनों कोण भी अलग अलग होंगे।
- इस त्रिभुज का परिमाप हम तीनों भुजाओं का योग करके निकाल सकते हैं।
- इस त्रिभुज के अंदर के कोण एक समकोण भी हो सकते हैं।
- इस त्रिभुज में समरूपता की कोई रेखा नहीं होती हैं।
- इस त्रिभुज की कोई समान भुजाएँ नहीं होती हैं।
- इसका कोई बिंदु समरूप नहीं होता हैं।
- तीनों भुजा के योग से परिमाप प्राप्त होता हैं।
- इस त्रिभुज में बड़े कोण के सामने की भुजा बड़ी तथा छोटे कोण के सामने की भुजा छोटी होती हैं।
- बड़ी भुजा का सम्मुख कोण बड़ा तथा छोटी भुजा का सम्मुख कोण छोटा होता हैं।
जरूर पढ़िए :
विषमबाहु त्रिभुज के उदाहरण
प्रश्न1. एक त्रिभुज की भुजाएं क्रमशः 3 सेंटीमीटर, 4 सेंटीमीटर और 5 सेंटीमीटर हैं इसका क्षेत्रफल क्या होगा?
A. 6 वर्ग सेंटीमीटर
B. 8 वर्ग सेंटीमीटर
C. 10 वर्ग सेंटीमीटर
D. 12 वर्ग सेंटीमीटर
हल:- प्रश्ननानुसार,
a = 3 सेंटीमीटर
b = 4 सेंटीमीटर
c = 5 सेंटीमीटर
त्रिभुज की तीनों भुजाओं का योग = (a + b + c)/2
s = (3 + 4 + 5)/2
s = 12/2
s = 6
त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ = √6(6 – 3)(6 – 4)(6 – 5)
∆ = √6 × 3 × 2 × 1
∆ = √36
∆ = 6
उत्तर:- 6 वर्ग सेंटीमीटर।
प्रश्न2. एक त्रिभुज जिसकी भुजा AB = 8 सेमी, भुजा BC =12 सेमी तथा भुजा AC = 16 सेमी हो तो क्या वह त्रिभुज विषमबाहु त्रिभुज कहा जायेगा।
हल:- प्रश्नानुसार,
A = क्षेत्रफल
s = त्रिभुज का अर्ध-परिमाप
a, b, c, क्रमशः त्रिभुज की भुजाये हैं।
विषमबाहु त्रिभुज का परिमाप = (a + b + c)/2
s = (16 + 12 + 20)/2
s = 48/2
s =24सेमी
A = √s (s – a) (s – b) (s – c)
A = √24 (24 – 16)(24 – 12)(24 – 20)
A = √24 × 8 × 12 × 4
A = √9,216
A = 96 सेमी.²
प्रश्न3. एक त्रिभुज की भुजाएं क्रमशः 12 सेंटीमीटर, 16 सेंटीमीटर, और 20 सेंटीमीटर हैं इसका क्षेत्रफल क्या होगा?
A. 92 वर्ग सेंटीमीटर
B. 94 वर्ग सेंटीमीटर
C. 96 वर्ग सेंटीमीटर
D. 98 वर्ग सेंटीमीटर
हल:- प्रश्ननानुसार,
a = 12 सेंटीमीटर
b = 16 सेंटीमीटर
c = 20 सेंटीमीटर
त्रिभुज की तीनों भुजाओं का योग = (a + b + c)/2
s = (12 + 16 + 20)/2
s = 48/2
s = 24
त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ = √24(24 – 12)(24 – 16)(24 – 20)
∆ = √24 × 12 × 8 × 4
∆ = √9216
∆ = 96
उत्तर:- 96 वर्ग सेंटीमीटर।
प्रश्न4. एक त्रिभुज की भुजाएं क्रमशः 35 सेंटीमीटर, 40 सेंटीमीटर, और 45 सेंटीमीटर हैं इसका क्षेत्रफल क्या होगा?
A. 512 वर्ग सेंटीमीटर
B. 862 वर्ग सेंटीमीटर
C. 610 वर्ग सेंटीमीटर
D. 750 वर्ग सेंटीमीटर
हल:- प्रश्ननानुसार,
a = 35 सेंटीमीटर
b = 40 सेंटीमीटर
c = 45 सेंटीमीटर
त्रिभुज की तीनों भुजाओं का योग = (a + b + c)/2
s = (35 + 40 + 45)/2
s = 120/2
s = 60
त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ = √60(60 – 35)(60 – 40)(60 – 45)
∆ = √60 × 25 × 20 × 15
∆ = √5,62,500
∆ = 750
उत्तर:- 750 वर्ग सेंटीमीटर।
जरूर पढ़िए :
उम्मीद हैं आपको विषमबाहु त्रिभुज की पोस्ट पसंद आयी होगीं।
यदि आपको ये आर्टिकल पसंद आया हो तो अपने दोस्तों के साथ जरूर शेयर करें।