इस पेज पर आप गणित के महत्वपूर्ण अध्याय समद्विबाहु त्रिभुज की जानकारी को पढ़ने वाले हैं।
पिछले पेज पर हमने समबाहु त्रिभुज की जानकारी शेयर की हैं तो उस पोस्ट को भी जरूर पढ़े।
चलिए इस पेज पर समद्विबाहु त्रिभुज की समस्त जानकारी को पढ़ते और समझते हैं।
Table of Contents
समद्विबाहु त्रिभुज की परिभाषा
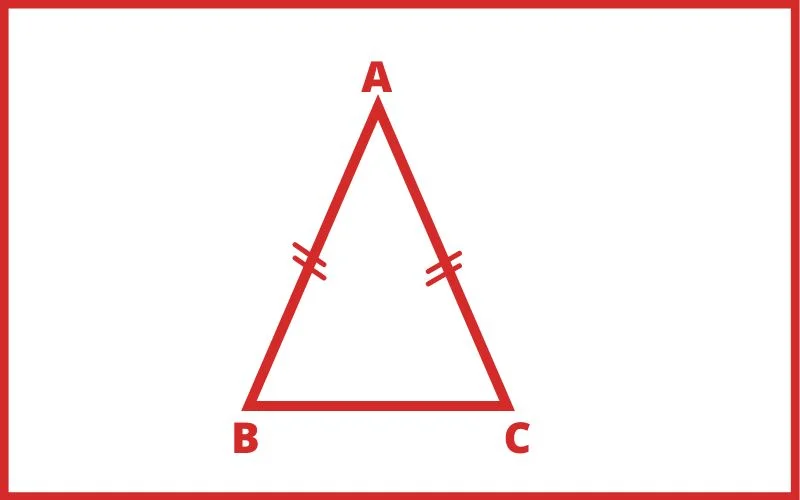
ऐसा त्रिभुज जिसकी तीन भुजाओं में से कोई दो भुजाएं समान होती हो समद्विबाहु त्रिभुज कहलाता हैं।
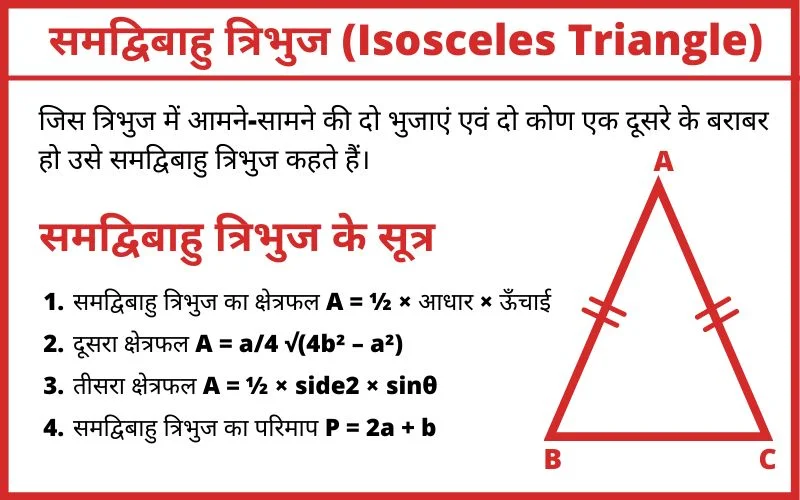
दूसरे शब्दों में – ऐसे त्रिभुज जिसकी दो भुजाएं एवं दो कोण आपस में बराबर हो समद्विबाहु त्रिभुज कहलाता हैं। अर्थात जिस त्रिभुज में आमने-सामने की दो भुजाएं एवं दो कोण एक दूसरे के बराबर हो उसे समद्विबाहु त्रिभुज कहते हैं।
समद्विबाहु त्रिभुज के सूत्र
- समद्विबाहु त्रिभुज का क्षेत्रफल A = ½ × आधार × ऊँचाई
क्षेत्रफल A = ½ × b × h - दूसरा क्षेत्रफल A = a/4 √(4b² – a²)
- तीसरा क्षेत्रफल A = ½ × side2 × sinθ
जहाँ θ = थीटा त्रिभुज का कोण हैं। - समद्विबाहु त्रिभुज का परिमाप P = 2a + b
जहाँ दो समान लम्बाई वाली भुजाएँ b हैं तथा आधार की भुजा a हैं।
समद्विबाहु त्रिभुज की विशेषताएं
- समद्विबाहु त्रिभुज की कोई भी दो भुजाएं बराबर होती हैं।
- समद्विबाहु त्रिभुज की असमान भुजा आधार होती है।
- त्रिभुज की दोनों समान भुजाओं के कोण भी समान होते है।
- शीर्ष से आधार पर डाला गया लम्ब आधार को समद्विभाजित करता है।
- आधार का लम्बार्द्धक शीर्ष से होकर जाता है।
- आधार का लम्बार्द्धक शीर्ष कोण को समद्विभाजित करता है।
जरूर पढ़िए :
समद्विबाहु त्रिभुज के प्रश्न
Q.1 उस समद्विबाहु त्रिभुज का परिमाप ज्ञात करो जिसकी भुजाओं का माप क्रमशः 3 सेंटीमीटर, 4 सेंटीमीटर, 4 सेंटीमीटर है।
A. 11 सेंटीमीटर
B. 21 सेंटीमीटर
C. 31 सेंटीमीटर
D. 41 सेंटीमीटर
हल:- प्रश्नानुसार,
a = 3, b = 4, b = 4
समद्विबाहु त्रिभुज के परिमाप का सूत्र = a + 2b
= 3 + 4 + 4
= 11 सेंटीमीटर
Ans. 11 सेंटीमीटर
Q.2 यदि एक समद्विबाहु त्रिभुज की तीनों भुजाओं का माप क्रमशः 8 सेंटीमीटर, 14 सेंटीमीटर, व 14 सेंटीमीटर है तो परिमाप ज्ञात कीजिए?
A. 10 सेंटीमीटर
B. 20 सेंटीमीटर
C. 36 सेंटीमीटर
D. 40 सेंटीमीटर
हल:- प्रश्नानुसार,
a = 8, b = 14, b = 14
समद्विबाहु त्रिभुज के परिमाप का सूत्र = a + 2b
= 8 + 14 + 14
= 36 सेंटीमीटर
Ans. 36 सेंटीमीटर
Q.3 उस समद्विबाहु त्रिभुज का क्षेत्रफल का ज्ञात कीजिए जिसकी भुजाएं क्रमश 8 सेंटीमीटर, 5 सेंटीमीटर और 8 सेंटीमीटर है?
A. 12 सेंटीमीटर
B. 20 सेंटीमीटर
C. 30 सेंटीमीटर
D. 40 सेंटीमीटर
हल:- प्रश्नानुसार,
दो समान भुजाओं का माप b = 8 सेंटीमीटर हैं।
असमान भुजा का माप a = 4 सेंटीमीटर हैं।
समद्विबाहु त्रिभुज का क्षेत्रफल = b/4 √4a² – b²
= 8/4 √[4 (5)² – 8²)]
= 2 √4 × 25 – 64
= 2 √100 – 64
= 2 √36
= 2 × 6
= 12
Ans. 12 सेंटीमीटर
Q.4 किसी समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात करो जिसकी तीनों भुजाओं का माप क्रमश: 10 सेंटीमीटर, 12 सेंटीमीटर, 12 सेंटीमीटर है?
A. 8 सेंटीमीटर
B. 24 सेंटीमीटर
C. 30 सेंटीमीटर
D. 48 सेंटीमीटर
हल:- प्रश्नानुसार,
दो समान भुजाओं का माप b = 12 सेंटीमीटर हैं।
असमान भुजा का माप a = 10 सेंटीमीटर हैं।
समद्विबाहु त्रिभुज का क्षेत्रफल = b/4 √4a² – b²
क्षेत्रफल = 12/4 [√4(10)² – (12)²]
क्षेत्रफल = 3 (√4 × 100 – 144)
क्षेत्रफल = 3√400 – 144
क्षेत्रफल = 3√256
क्षेत्रफल = 3 × 16
क्षेत्रफल = 48
Ans. 48 सेंटीमीटर
Q.5 किसी समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात करो जिसकी तीनों भुजाओं का माप क्रमश: 26 सेंटीमीटर, 48 सेंटीमीटर, 48 सेंटीमीटर है?
A. 140 सेंटीमीटर
B. 240 सेंटीमीटर
C. 300 सेंटीमीटर
D. 480 सेंटीमीटर
हल:- प्रश्नानुसार,
दो समान भुजाओं का माप b = 48 सेंटीमीटर हैं।
असमान भुजा का माप a = 26 सेंटीमीटर हैं।
समद्विबाहु त्रिभुज का क्षेत्रफल = 48/4 √4a² – b²
क्षेत्रफल = 12 [√4(26)² – (48)²]
क्षेत्रफल = 12 (√4 × 676 – 2304)
क्षेत्रफल = 12√2704 – 2304
क्षेत्रफल = 12√400
क्षेत्रफल = 12 × 20
क्षेत्रफल = 240
Ans. 240 सेंटीमीटर
जरूर पढ़िए :
उम्मीद हैं आपको समद्विबाहु त्रिभुज की पोस्ट पसंद आयी होगीं।
यदि आपको ये आर्टिकल पसंद आया हो तो अपने दोस्तों के साथ जरूर शेयर करें।