इस पेज पर आप हीरोन का सूत्र से सम्बंधित जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।
पिछले पर हमने पाइथागोरस प्रमेय और थेल्स प्रमेय की जानकारी शेयर की हैं तो आप उन आर्टिकल को भी पढ़े।
चलिए आज हम हीरोन का सूत्र क्या हैं और इसके सवालों को किस प्रकार हल किया जाता हैं की समस्त जानकारी पढ़ते और समझते हैं।
Table of Contents
हीरोन का सूत्र किसे कहते हैं
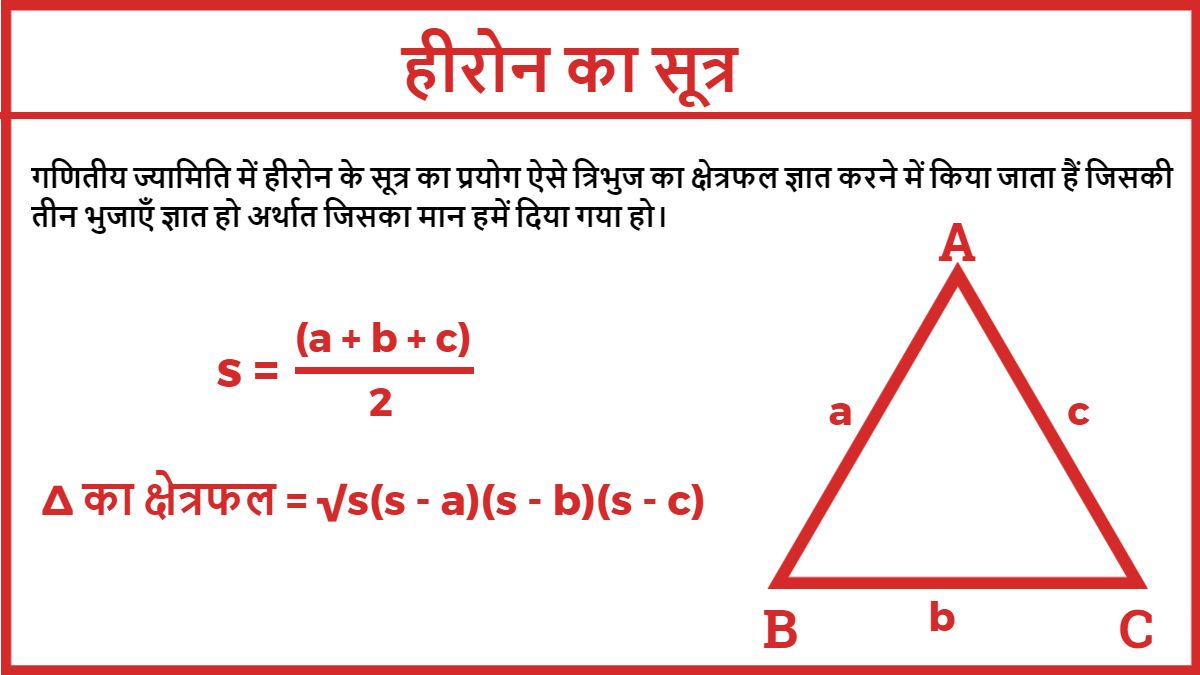
गणितीय ज्यामिति में हीरोन के सूत्र का प्रयोग ऐसे त्रिभुज का क्षेत्रफल ज्ञात करने में किया जाता हैं जिसकी तीन भुजाएँ ज्ञात हो अर्थात जिसका मान हमें दिया गया हो।
उपयोग के अनुसार इसे “हीरो का सूत्र” भी कहते हैं क्योंकि इसका नाम हीरो ऑफ अलेक्जेंड्रिया पर पड़ा है जो एक महान गणितज्ञ थे।
हीरोन के सूत्र को समझने के लिए हमें त्रिभुज की जानकारी होना आवश्यक हैं। इस फार्मूला का प्रयोग त्रिभुज के साथ-साथ चतुर्भुज, बहुभुज, त्रिकोणमिति आदि जैसे क्षेत्रों में किया जाता है।
हीरोन का सूत्र का प्रयोग करने में त्रिभुज या चतुर्भुज की कोण ज्ञात करने की आवश्यकता नही होती यह सूत्र केवल भुजाओं की लम्बाई पर कार्य करता है।
त्रिभुज किसे कहते हैं
तीन भुजाओं से घिरी आकृति को त्रिभुज कहते हैं।
किसी त्रिभुज में तीन शीर्ष, तीन भुजाएँ, तीन कोण होते हैं।
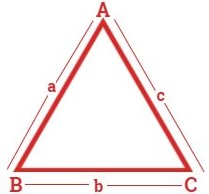
∆ABC में,
शीर्ष :- A, B, C और कोण ∠A, ∠B, ∠C हैं जिनके नाम ∠BAC, ∠ABC, ∠ACB हैं।
Note:- ∠ चिन्ह का प्रयोग कोण दर्शाने के लिए किया जाता हैं।
त्रिभुज की भुजाएँ :-
AB या BA
BC या CB
AC या CA
हिरोन का सूत्र
∆ का क्षेत्रफल = √s(s – a)(s – b)(s – c)
यहाँ पर S = ∆ का अर्द्ध परिमाप
a, b, c = ∆ की भुजाएँ
s = (a + b + c)/2
a, b, एवं c त्रिभुज तीनों भुजाओं की लम्बाई है।
Note:-
- विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए हीरोन के सूत्र का प्रयोग किया जाता है।
- सामान्य रूप से त्रिभुज के मूल रूप का भी प्रयोग क्षेत्रफल ज्ञात करने के लिए होता है।
हिरोन के सूत्र से सम्बंधित महत्वपूर्ण बिंदु
- यदि a, b और c त्रिभुज की तीन भुजाएँ हो, तो अर्द्धपरिमाप, s = (a + b + c)/2 होता है।
- हीरो ऑफ अलेक्जेंड्रिया के नाम पर हीरोन का सूत्र नाम पड़ा था।
- चतुर्भुजों का क्षेत्रफल निकालने के लिए हीरोन का सूत्र का प्रयोग किया जा सकता है।
- हीरोन का सूत्र चक्रीय चतुर्भुज का क्षेत्रफल निकालने के लिए ब्रह्मगुप्त के सूत्र की एक विशेष परिमाण है।
हिरोन के सूत्र से सम्बंधित उदाहरण
Q.1 एक त्रिभुज की भुजाएँ 3, 4 तथा 5 सेंटीमीटर हैं त्रिभुज का क्षेत्रफल बताइए?
हल:- दिया है,
त्रिभुज के तीनों भुजाएँ क्रमशः
a = 3 सेंटीमीटर,
b = 4 सेंटीमीटर
c = 5 सेंटीमीटर
अर्द्धपरिमाप = (a + b + c)/2
s = (3 + 4 + 5)/2
s = 12/2
s = 6
अतः त्रिभुज का क्षेत्रफल = √[s(s – a)(s – b)(s – c)]
= √[(6(6 – 3)(6 – 4)(6 – 5)]
= √(6 × 3 × 2 × 1)
= √36 cm²
= 6 सेंटीमीटर
त्रिभुज का क्षेत्रफल = 6 सेंटीमीटर²
Q.2 एक त्रिभुज का क्षेत्रफल निकालिए जिसकी तीनों भुजाएँ क्रमशः 4 सेंटीमीटर, 6सेंटीमीटर और 8सेंटीमीटर हो?
हल:- दिया है,
त्रिभुज के तीनों भुजाएँ क्रमशः
a = 4 सेंटीमीटर,
b = 6 सेंटीमीटर
c = 8 सेंटीमीटर
अर्द्धपरिमाप = (a + b + c)/2
s = (4 + 6 + 8)/2
s = 18/2
s = 9
अतः त्रिभुज का क्षेत्रफल = √[s(s – a)(s – b)(s – c)]
= √[(9(9 – 4)(9 – 6)(9 – 8)]
= √9 × 5 × 3 × 1
= 3√ 5 × 3 × 1
A = 3√15 सेंटीमीटर²
Q.3 एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 8 सेंटीमीटर और 11 सेंटीमीटर है और जिसका परिमाप 32 सेंटीमीटर हैं।
हल:- दिया है,
परिमाप = 32 cm,
a = 8 cm और b = 11
इसीलिए, तीसरी भुजा = 32 – (8 + 11)
= 32 – 19
c = 13 cm
अर्ध परिमाप = 32/2
= 16
अतः त्रिभुज के क्षेत्रफल = √[s(s – a)(s – b) (s – c)]
= √[(16(16 – 8)(16 – 11)(16 – 13)]
= √16 × 8 × 5 × 3
= √1920 cm²
अतः क्षेत्रफल = √1920 सेंटीमीटर²
Ans. √1920 सेंटीमीटर²
Q.4 एक त्रिभुज का क्षेत्रफल ज्ञात करें जिसके दो भुजाएँ 18 सेंटीमीटर और 10 सेंटीमीटर हैं और परिधि 42 सेंटीमीटर है।
हल :- माना, कि त्रिकोण का तीसरा भुजा “x” है,
अब, त्रिभुज की तीन भुजाएँ 18 सेमी, 10 सेमी और x सेंटीमीटर हैं
यह दिया जाता है कि त्रिभुज की परिधि = 42 सेंटीमीटर तो,
x = 42 – (18 + 10) सेंटीमीटर
= 14 सेंटीमीटर
त्रिभुज की अर्ध परिधि = 42/2
= 21 सेंटीमीटर
हीरोन के सूत्र का उपयोग करेंगे,
त्रिभुज का क्षेत्रफल, = √[s(s – a)(s – b)(s – c)]
= √[21 (21 – 18) (21 – 10) (21 – 14)] सेंटीमीटर ²
= √21 × 3 × 11 × 7 सेंटीमीटर ²
= √441 × 11
= 21√11 सेंटीमीटर ²
Ans. 21√11 सेंटीमीटर²
Q.5 एक त्रिभुज की भुजाएँ 12 : 17 : 25 के अनुपात में हैं और इसकी परिधि 540 सेंटीमीटर है। इसका क्षेत्रफल ज्ञात कीजिए।
हल :- त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है
अब त्रिभुज की भुजाओं के बीच का सामान्य अनुपात x होने दें
भुजाएँ 12x, 17x और 25x हैं
यह भी दिया जाता है कि त्रिकोण की परिधि = 540 सेंटीमीटर
12x + 17x + 25x = 540 सेंटीमीटर
54x = 540 सेंटीमीटर
x = 540/54
तो, x = 10
12x = 12 × 10 = 120
17x = 17 × 10 = 170
25x = 25 × 10 = 250
अब त्रिभुज की भुजाएँ 120 सेंटीमीटर, 170 सेंटीमीटर, 250 सेंटीमीटर हैं।
तो त्रिभुज की अर्ध परिधि = 540/2
= 270 सेंटीमीटर
त्रिभुज का क्षेत्रफल = √[s(s – a)(s – b)(s – c)]
= √270 (270 – 120)(270 – 170)(270 – 250)
= √270 × 150 × 100 × 20
= √81,000,000
= 9000 सेंटीमीटर²
Ans. 9000 सेंटीमीटर²
Q.6 7 प्रति वर्ग मीटर की दर से 50 मीटर, 65 मीटर और 65 मीटर की भुजाओं के त्रिभुजाकार क्षेत्र में घास बिछाने की लागत ज्ञात कीजिए।
हल:- प्रश्नानुसार,
त्रिकोणीय क्षेत्र की साइड्स 50 मीटर, 65 मीटर और 65 मीटर हैं।
एक त्रिकोणीय क्षेत्र में घास बिछाने की लागत = 2 रुपये प्रति मी
a = 50, b = 65, c = 65
s = (a + b + c)/2
s = (50 + 65 + 65)/2
s = 180/2
s = 90
त्रिभुज का क्षेत्रफल = √s (s – a) (s – b) (s – c))
= √90 (90-50) (90-65) (90-65)
= √(90 × 40 × 25 × 25)
= 1500 मी²
घास बिछाने की लागत = त्रिकोण का क्षेत्रफल × लागत प्रति मी²
= 1500 × 7
= 10.500 रु.
Ans. 10.500 रु.
जरूर पढ़िए :
उम्मीद हैं आपको हीरोन का सूत्र की समस्त जानकारी पसंद आयी होंगी।
यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ जरूर शेयर करें।