इस पेज पर हम फलन, सीमा तथा सांतत्य की जानकारी को उदाहरण सहित पढ़ेगें तो इस पोस्ट को पूरा जरूर पढ़िए।
पिछले पेज पर हम प्रतिलोम त्रिकोणमितीय फलन की जानकारी शेयर कर चुके हैं यदि आपने उस आर्टिकल को नहीं पढ़ा तो उसे भी जरूर पढ़े।
चलिए आज हम फलन, सीमा तथा सांतत्य की जानकारी को पढ़ते और समझते हैं।
Table of Contents
फलन, सीमा तथा सांतत्य की कुछ परिभाषाएँ
(A). संबद्ध राशियाँ
जब दो राशियाँ इस प्रकार हो कि एक राशि का मान परिवर्तित करने पर दूसरी राशि भी परिवर्तित हो, अर्थात एक राशि का मान दूसरी राशि पर निर्भर करता हो तो ऐसी राशियाँ संबद्ध राशियाँ कहलाती हैं।
उदाहरण :-
(i). किसी वर्ग का क्षेत्रफल (A = l) उस वर्ग की भुजा की लम्बाई (l) पर निर्भर करता हैं, जैसे-जैसे भुजा की लम्बाई घटती या बढ़ती हैं वैसे-वैसे वर्ग का क्षेत्रफल भी घटता या बढ़ता हैं।
(ii). किसी गोले का आयतन (V = ⁴⁄₃ πr²) उसकी त्रिज्या (r) पर निर्भर करती हैं।
(iii). किसी संख्या का घन (k = x³) स्वयं उस संख्या (x) पर निर्भर करता हैं।
(B). चर
वह राशि, जिसका मान गणितीय संक्रियाओं में बदलता रहता हैं, चर कहलाती हैं।
चर राशियों को x, y, z, u, v………….. से प्रदर्शित किया जाता हैं।
चर दो प्रकार के होते हैं।
- स्वतंत्र चर
- परतन्त्र चर
(i). स्वतंत्र चर :- जो कोई निर्दिष्ट मान ग्रहण कर सकता हैं उस चर को स्वतन्त्र चर कहते हैं।
(ii). परतन्त्र चर :- जिसका मान स्वतन्त्र चर के मान पर निर्भर करता हैं उस चर को परतन्त्र चर कहते हैं।
(C). अचर
अचर उस राशि को कहते हैं जो गणितीय संक्रियाओं में अपरिवर्तित रहती हैं।
अचर को प्रायः a, b, c,………….. से व्यक्त किया जाता हैं।
अचर दो प्रकार के होते हैं।
- निरपेक्ष अचर
- स्वेच्छ अचर
(i). निरपेक्ष अचर :- वह अचर, जिसका मान प्रत्येक गणितीय संक्रियाओं में वहीं बना रहता हैं, निरपेक्ष अचर कहलाता हैं।
जैसे :- 1, 2, 3, π, √5
(ii). स्वेच्छ अचर :- वह अचर, जिसका मान एक विशेष संक्रिया में नियत रहता हैं, किन्तु संदर्भ बदलने पर जिसका मान बदल जाता हैं, स्वेच्छ अचर कहलाता हैं।
फलन
यदि दो चर x और y इस प्रकार सम्बंधित हो कि x के प्रत्येक मान के लिए y का एक निशिचत मान हो, तो y को x का फलन कहते हैं।
y = 3x² + 5
| x | 0 | 1 | 2 | …… …… |
| y | 5 | 8 | 17 | …… …… |
x के प्रत्येक निशिचत मान के लिए y का संगत निश्चित मान हैं। अतः y, x का फलन हैं।
इसे निम्न प्रकार से व्यक्त करते हैं।
y = f (x)
इसे पढ़ते हैं “y बराबर x का फलन”
f के स्थान पर F, φ, ψ, g,……….. इत्यादि अक्षरों का प्रयोग किया जाता हैं।
जैसे :-
y = F(x), y = φ(x), y = ψ(x), y = δ(x)
फलन का मान,
माना y = f(x)
तो x = a के लिए
y = f(a)
f(a) को फलन f(x) का मान कहते हैं, जब x = a हो।
उदाहरण : माना
y = 4x³ − 3x² + 1
y = f(x)
f(x) = 4x³ – 3x² + 1
x = 2 रखने पर
f(2) = 4(2)³ – 3(2)² + 1
= 32 – 12 + 1
21
अतः x = 2 पर फलन का मान 21 हैं।
फलन, सीमा तथा सांतत्य के प्रश्नों के हल
Q 1. यदि f(x) = log x, हो तो f(1) का मान ज्ञात कीजिए ?
हल :- प्रश्नानुसार,
f(x) = log x,
x = 1 रखने पर
f(1) = log 1 = 0
Ans. 0
Q 2. यदि f(x) = 1 + sin x, हो तो f(π/₃) का मान ज्ञात कीजिए ?
हल :- प्रश्नानुसार,
f(x) = 1 + sin x
f(π/₃) = 1 + sin π/₃
f(π/₃) = 1 + sin 60°
Ans. 1 + √3/2
Q 3. यदि f(x) = x³ + 3x – 4sin³x हो तो सिद्ध कीजिए कि f(x), x का विषम फलन हैं?
हल :- प्रश्नानुसार,
f(x) = x³ + 3x – 4sin³x ……………..(i)
समीकरण (i) में x = -x रखने पर,
f(-x) = (-x)³ + 3(-x) – 4sin³(-x)
= -x³ – 3x – 4 {-sin³-x}
= -x³ – 3x + 4sin³x
= -(x³ + 3x – 4sin³x)
f (x) = – f(x) [समीकरण (i) से]
अतः f (x), x का विषम फलन हैं यदि सिद्ध करना था।
Q 4. यदि f(x) = x² + 2x Sin x + 3 हो, तो सिद्ध कीजिए कि f(x), x का एक सम फलन हैं?
हल :- प्रश्नानुसार,
f(x) = x² + 2x Sin x + 3 ……………..(i)
समीकरण (i) में x = -x रखने पर,
f(-x) = (-x)² + 2 (-x) Sin (-x) + 3
= x² + 2x Sin x + 3
f (-x) = f(x) [समीकरण (i) से]
अतः f (x), x का सम फलन हैं यदि सिद्ध करना था।
Q.5 Cos⁻¹ (3x – 1) का प्रान्त ज्ञात कीजिए ?
हल :- प्रश्नानुसार,
Cos⁻¹ (3x – 1)
माना, f(x) = Cos⁻¹ (3x – 1)
-1 ≼ 3x – 1 ≼ 1
1 + 1 ≦ 3x − 1 + 1 ≼ 1 + 1
0 ≼ 3x ≼ ⅔
0 ≼ x ≼ ⅔
f(x) = 0 ≾ x ≾ ⅔ = [0, ⅔]
Q.6 यदि f(x) = x² − 4x + 6 हो, तो f (2 + x) का मान ज्ञात कीजिए ?
हल :- प्रश्नानुसार,
f(x) = x² − 4x + 6
x = 2 + x
f(2 + x ) = (2 + x)² − 4(2 + x) + 6
= 4 + x² + 4x − 8 − 4x + 6
= x² + 2
Q.7 निम्न फलनों के ग्राफ खींचिए ?
(i). y = 3
(ii). y = 0
(iii). y = -3
(i). y = 3
हल :- (i) x के भिन्न-भिन्न मानों के लिए y के संगत मान प्राप्त करने पर हम देखेंगे कि x के प्रत्येक मान के लिए y = 3 (अचर) प्राप्त होगा।
x और y के कुछ संगत मान निम्नानुसार हैं।
| x | 0 | 1 | 2 | 3 |
| y | 3 | 3 | 3 | 3 |
बिंदुओं (0, 3), (1, 3), (2, 3), (3, 3) को ग्राफ पेपर पर अंकित कर मिलाने पर हमें दिये हुए फलन y = 3 का एक ग्राफ प्राप्त होता हैं।
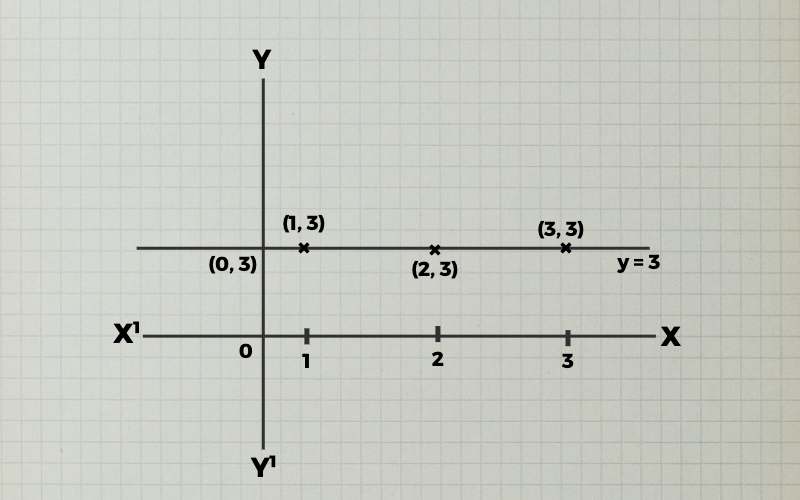
नोट : हम जानते हैं की y = 3 सरल रेखा का समीकरण हैं जो Y-अक्ष पर अंतखंड 3 काटती हैं तथा X-अक्ष के समानांतर होती हैं।
(ii). y = 0
| x | 0 | 1 | 2 | 3 |
| y | 0 | 0 | 0 | 0 |
बिंदुओं (0, 0), (1, 0), (2, 0), (3, 0) को ग्राफ पेपर पर अंकित कर मिलाने पर हमें दिये हुए फलन y = 0 का एक ग्राफ प्राप्त होता हैं।
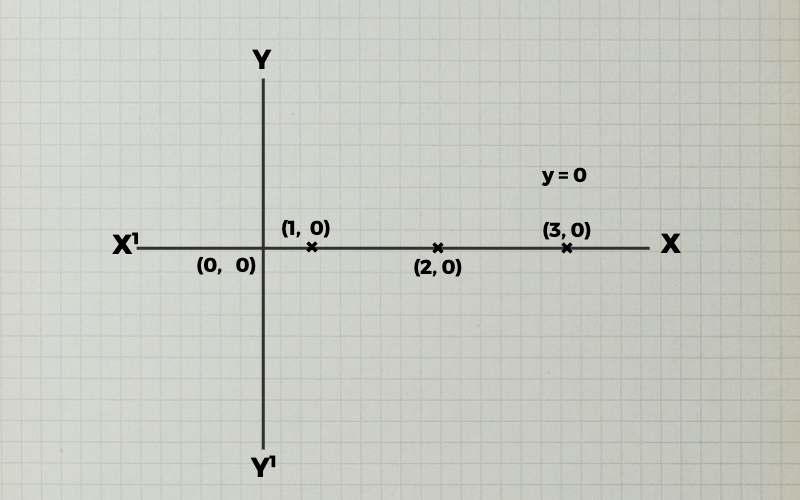
नोट : हम जानते हैं की y = 0, X अक्ष समीकरण को प्रदर्शित करता हैं।
(iii). y = -3
| x | 0 | 1 | 2 | 3 |
| y | -3 | -3 | -3 | -3 |
बिंदुओं (0, -3), (1, -3), (2, -3), (3, -3) को ग्राफ पेपर पर अंकित कर मिलाने पर हमें दिये हुए फलन y = 0 का एक ग्राफ प्राप्त होता हैं।
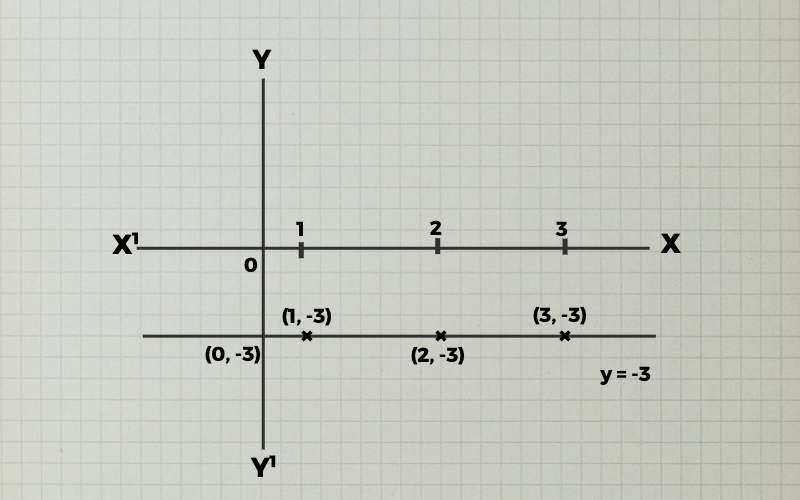
नोट : ग्राफ एक सरल रेखा प्रदर्शित करता हैं जो कि X-अक्ष के नीचे हैं परन्तु उसके समांतर हैं।
Q. 8 यदि f और g के डोमेन R हो तो f – g का मान ज्ञात कीजिए जहाँ f(x) = x³ तथा g(x) = x² – 1.
हल :- (f − g) x = f(x) – g(x)
= x³ − (x² – 1)
= x³ – x² + 1,
∀ x ⋲ R.
उम्मीद हैं आपको फलन, सीमा तथा सांतत्य की जानकारी पसंद आयी होगी यदि आपको यह जानकारी पसंद आयी हो तो इस आर्टिकल को अपने दोस्तों के साथ जरूर शेयर कीजिए।

