लघुत्तम समापवर्त्य और महत्तम समापवर्तक की परिभाषा

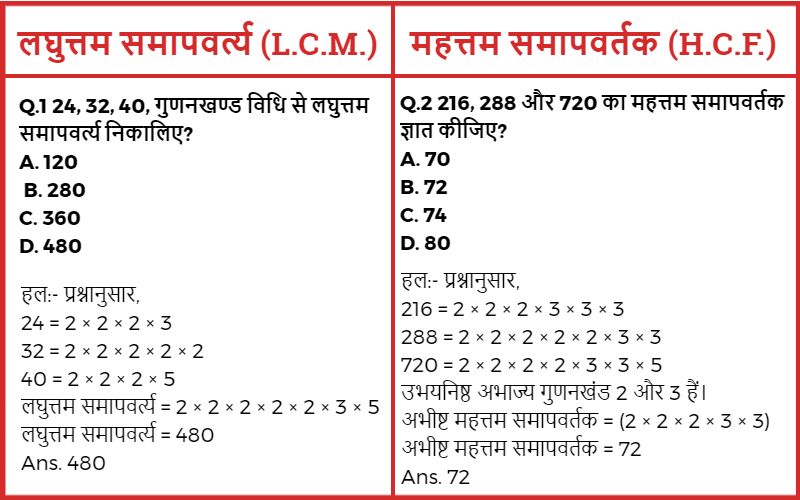
इस पेज पर आप लघुत्तम समापवर्त्य और महत्तम समापवर्तक की सम्पूर्ण जानकारी पड़ेगें।

पिछले पेज पर हमने संख्या पद्धति की समस्त जानकारी शेयर की हैं तो इस पोस्ट को भी पढ़े।

चलिए इस पेज पर लघुत्तम समापवर्त्य और महत्तम समापवर्तक की जानकारी पढ़ते और समझते हैं लघुत्तम समापवर्त्य और महत्तम समापवर्तक।

लघुत्तम समापवर्त्य की परिभाषा

दो या दो से अधिक संख्याओं का लघुत्तम समापवर्त्य वह छोटी से छोटी संख्या हैं जो उन संख्याओं से पूरी तरह विभाजित हो जाती हैं।

जैसे :- 4, 8, 12 का लघुत्तम समापवर्त्य = 2 × 2 × 2 × 3 = 24,

अतः अभीष्ट लघुत्तम समापवर्त्य 24 वह छोटी से छोटी संख्या हैं जो 4, 8, 12 तीनों से पूरी-पूरी तरह विभाजित हो जाती हैं।

लघुत्तम समापवर्त्य निकालने का तरीका

• अभाज्य गुणनखण्ड विधि द्वारा
• भाग विधि द्वारा

(a). अभाज्य गुणनखण्ड विधि द्वारा

सर्वप्रथम दी गई संख्या को अभाज्य गुणनखण्डों के रूप में व्यक्त करें। फिर इन संख्याओं के सभी अभाज्य गुणनखण्डों के सबसे बड़े घातांकों वाली संख्याओं का प्राप्त गुणनखण्ड ही लघुत्तम समापवर्त्य हैं।

उदाहरण 1. 32, 64 तथा 128 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- प्रश्नानुसार,
32 ⇒ 2 × 2 × 2 × 2 × 2 = 2⁵
64 ⇒ 2 × 2 × 2 × 2 × 2 × 2 = 2⁶
48 ⇒ 2 × 2 × 2 × 2 × 3 = 2⁴ × 3¹
लघुत्तम समापवर्त्य = 2, 3 की सबसे बड़े घातांकों वाली संख्याओं का गुणनफल = 2⁶ × 3¹
लघुत्तम समापवर्त्य = 96

उदाहरण 2. 12, 48, 72 तथा 120 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- प्रश्नानुसार,
12 = 2 × 2 × 3 = 2² × 3¹
48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3¹
72 = 2 × 2 × 2 × 3 × 3 = 2³ × 3²
120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3¹ × 5¹
लघुत्तम समापवर्त्य = 2, 3 तथा 5 की सबसे बड़ी घातों वाली संख्याओं का गुणनफल = 2⁴ × 3² × 5¹
लघुत्तम समापवर्त्य = 16 × 9 × 5
लघुत्तम समापवर्त्य = 720
Ans. 720

(b). भाग विधि द्वारा

उदाहरण 3. 24, 48, 96, 192 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

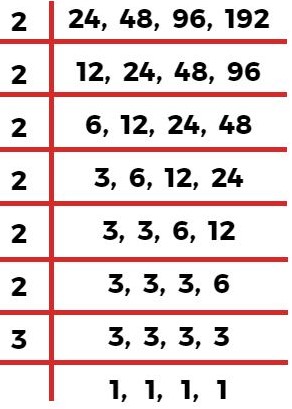
लघुत्तम समापवर्त्य = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁶ × 3¹
लघुत्तम समापवर्त्य = 192

उदाहरण 4. 32, 56, 78, 120 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

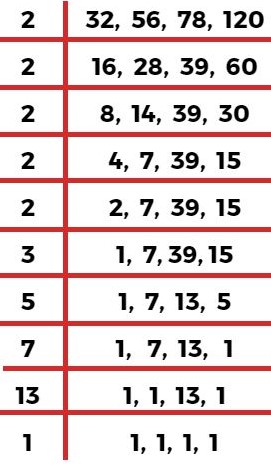
लघुत्तम समापवर्त्य = 2 × 2 × 2 × 2 × 2 × 3 × 5 × 7 × 13
लघुत्तम समापवर्त्य = 32 × 15 × 91
लघुत्तम समापवर्त्य = 43,680

1. भिन्नों का लघुत्तम समापवर्त्य

भिन्नों का लघुत्तम समापवर्तक (L.C.M.) = अंशों का लघुत्तम समापवर्त्य / हरों का महत्तम समापवर्तक

उदाहरण 5. 7/9, 14/15 तथा 7/10 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- प्रश्ननानुसार,
दी गई भिन्नों का लघुत्तम समापवर्त्य = 7, 14, 7 का लघुत्तम समापवर्त्य / 9, 15, 10 का महत्तम समापवर्तक
= 14/1
= 14

उदाहरण 6. 2/5, 3/4, 1/9 तथा 7/10 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- प्रश्ननानुसार,
दी गई भिन्नों का लघुत्तम समापवर्त्य = 2, 3, 1, 7 का लघुत्तम समापवर्त्य / 5, 4, 9, 10 का महत्तम समापवर्तक
= 42/1
= 42

2. घातांक का लघुत्तम समापवर्त्य

(a). जब दी गयी संख्याओं का आधार समान हो, तो सर्वाधिक घात वाली संख्या ही दिए गए संख्याओं का लघुत्तम समापवर्त्य होगा।

उदाहरण 7. 5¹, 5², 5⁴, 5⁶ तथा 5¹² का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- समान आधार पर 5 हैं। तथा अधिकतम घात 5¹² का हैं।
लघुत्तम समापवर्त्य = 5¹²

उदाहरण 8. 5⁻¹, 5⁻², 5⁻⁴, 5⁻⁶ तथा 5⁻¹² का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- आधार 5 समान हैं तथा अधिकतम घात 5⁻¹ की हैं।
लघुत्तम समापवर्त्य = 5⁻¹

(b). जब आधार समान नहीं हो तथा आधार में कोई उभयनिष्ठ गुणन खण्ड नहीं हो, तो दिए गए संख्याओं का गुणनखण्ड ही लघुत्तम समापवर्त्य होगा।

उदाहरण 9. 5³ तथा 2³ का लघुत्तम समापवर्त्य = 5³ × 2³
लघुत्तम समापवर्त्य = 5 × 5 × 5 × 2 × 2 × 2
लघुत्तम समापवर्त्य = 125 × 8
लघुत्तम समापवर्त्य = 1000

3. दशमलव संख्याओं का लघुत्तम समापवर्त्य

(a). सबसे पहले दशमलव के बाद अधिकतम अंकों वाली संख्या का पता लगाइए।

(b). यदि दशमलव के बाद अधिकतम दो अंक हो, तो सभी अंकों में 100 से गुणा करके उसे पूर्ण संख्या में बदल देगें।

अगर दशमलव के बाद अधिकतम तीन, चार या पाँच अंक हो, तो उसमें क्रमशः 1000, 10000 या 100000 से गुणा करके उसे पूर्ण संख्या में बदल देगें।

(c). प्राप्त पूर्ण संख्याओं का लघुत्तम समापवर्त्य ज्ञात करेंगें। उसके बाद प्राप्त लघुत्तम समापवर्त्य में 100, 1000, 10000 से गुणा किया गया था। भाग देने के बाद जो संख्या प्राप्त होगी वही दी गई संख्याओं का लघुत्तम समापवर्त्य होगा।

उदाहरण10. 0.12, 4.8, 0.72 तथा 1.20 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- यहाँ दशमलव के बाद अधिकतम दो अंक हैं। इसलिए सभी संख्याओं को 100 से गुणा करने पर प्राप्त संख्या = 12, 480, 72, 120

इन संख्याओं का लघुत्तम समापवर्त्य = 1440
अभीष्ट लघुत्तम समापवर्त्य = 1440/100
लघुत्तम समापवर्त्य = 14.40

महत्तम समापवर्तक की परिभाषा

दो से अधिक संख्याओं का महत्तम समापवर्तक वह बड़ी से बड़ी संख्या हैं जिसमें वह सभी संख्याएँ पूरी-पूरी विभाजित हो जाती हैं।

जैसे:- 4, 8, 12 का महत्तम समापवर्तक 4 हैं।

महत्तम समापवर्तक निकालने का तरीका

• अभाज्य गुणनखण्ड विधि
• द्वारा भाग विधि द्वारा

(a). अभाज्य गुणनखण्ड विधि द्वारा

सर्वप्रथम दी गई प्रत्येक संख्या को अभाज्य गुणनखण्डों के गुणनफल के रूप में लिखिए।

उभयनिष्ठ अभाज्य गुणनखण्डों की छोटी से छोटी घातों वाले गुणनखण्डों का गुणनफल ही प्राप्त संख्याओं का महत्तम समापवर्तक होगा।

उदाहरण 1. 8, 36 तथा 72 का महत्तम समापवर्तक ज्ञात कीजिए?

हल:- प्रश्ननानुसार,
8 ⇒ 2 × 2 × 2 = 2³
36 ⇒ 2 × 2 × 3 × 3 = 2² × 2²
72 ⇒ 2 × 2 × 2 × 3 × 3 = 2³ × 2²
उभयनिष्ट अभाज्य गुणनखण्ड = 2
महत्तम समापवर्तक = सबसे छोटी घातांकों वाली संख्याओं का गुणनफल = 2²
महत्तम समापवर्तक = 4

उदाहरण 2. 48, 36 तथा 72 का महत्तम समापवर्तक ज्ञात कीजिए?

हल:- प्रश्नानुसार,
48 ⇒ 2 × 2 × 2 × 2 × 3 = 2⁴ × 3¹
36 ⇒ 2 × 2 × 3 × 3 = 2² × 3²
72 ⇒ 2 × 2 × 2 × 3 × 3 = 2³ × 3²
उभयनिष्ट अभाज्य गुणनखण्ड = 2, 3
महत्तम समापवर्तक = 2, 3 तथा 5 की सबसे छोटी घातों वाली संख्याओं का गुणनफल = 2² × 3¹
महत्तम समापवर्तक = 4 × 3
महत्तम समापवर्तक = 12
Ans. 12

(b). भाग विधि द्वारा

माना दो संख्याओं x और y का महत्तम समापवर्तक ज्ञात करना हैं। जबकि (y > x) → y, x से बड़ा हैं। बड़ी संख्याओं में छोटी संख्या से भाग देगें।

उदाहरण 3. 8, 36 और 72 का महत्तम समापवर्तक ज्ञात कीजिए?

उदाहरण 4. 48, 36 और 72 का महत्तम समापवर्तक ज्ञात कीजिए?

1. भिन्नों का महत्तम समापवर्तक

भिन्नों का महत्तम समापवर्तक (L.C.M.) = अंशों का महत्तम समावतर्क / हरों का लघुत्तम समापवर्त्य

उदाहरण 5. 5/6, 5/8, 10/21 तथा 2/3 का महत्तम समापवर्तक ज्ञात कीजिए?

हल:- प्रश्ननानुसार,
दी गई भिन्नों का महत्तम समापवर्तक = 5, 5, 10 और 2 का महत्तम समापवर्तक / 6, 8, 21 और 3 का लघुत्तम समापवर्त्य
महत्तम समापवर्तक = 1/168

उदाहरण 6. 1/7, 2/3, 4/5 तथा 5/7 का लघुत्तम समापवर्त्य ज्ञात कीजिए?

हल:- प्रश्ननानुसार,
दी गई भिन्नों का महत्तम समापवर्तक = 1, 2, 4 और 5 का महत्तम समापवर्तक / 7, 3, 5 और 7 का लघुत्तम समापवर्त्य
महत्तम समापवर्तक = 1/105

2. घातांक का महत्तम समापवर्तक

(a). जब दी गयी संख्याओं का आधार समान हो, तो सर्वाधिक घात वाली संख्या ही दिए गए संख्याओं का महत्तम समापवर्तक होगा।

उदाहरण 7. 7², 7⁹, 7¹⁴ तथा , 7³² का महत्तम समापवर्तक ज्ञात कीजिए?

हल:- समान आधार पर 7 हैं। तथा न्यूनतम घात 7² का हैं।
महत्तम समापवर्तक = 7²

उदाहरण 8. 5⁻¹, 5⁻², 5⁻⁴, 5⁻⁶ तथा 5⁻¹² का महत्तम समापवर्तक ज्ञात कीजिए?

हल:- आधार 8 समान हैं तथा न्यूनतम घात 8⁻¹² की हैं।
महत्तम समापवर्तक = 8⁻¹²

(b). जब आधार समान नहीं हो तथा आधार में कोई उभयनिष्ठ गुणन खण्ड नहीं हो, तो दिए गए संख्याओं का गुणनखण्ड ही महत्तम समापवर्तक 1 होगा।

उदाहरण 9. 2³, 4² और 8² का महत्तम समापवर्तक ज्ञात कीजिए?

चूँकि आधार (2) समान हैं इसलिए महत्तम समापवर्तक 1 नहीं होगा। इसका महत्तम समापवर्तक 8 होगा।

3. दशमलव संख्याओं का महत्तम समापवर्तक

(a). सबसे पहले दशमलव के बाद अधिकतम अंकों वाली संख्या का पता लगाइए।

(b). यदि दशमलव के बाद अधिकतम दो अंक हो, तो सभी अंकों में 100 से गुणा करके उसे पूर्ण संख्या में बदल देगें।

अगर दशमलव के बाद अधिकतम तीन, चार या पाँच अंक हो, तो उसमें क्रमशः 1000, 10000 या 100000 से गुणा करके उसे पूर्ण संख्या में बदल देगें।

(c). प्राप्त पूर्ण संख्याओं का महत्तम समापवर्तक ज्ञात करेंगें। उसके बाद प्राप्त महत्तम समापवर्तक में 100, 1000, 10000 से गुणा किया गया था। भाग देने के बाद जो संख्या प्राप्त होगी वही दी गई संख्याओं का महत्तम समापवर्तक होगा।

उदाहरण10. 0.05, 0.10, तथा 0.025 का महत्तम समापवर्तक ज्ञात कीजिए?

हल:- यहाँ दशमलव के बाद अधिकतम तीन अंक हैं। इसलिए सभी संख्याओं को 1000 से गुणा करने पर प्राप्त संख्या = 50, 100, तथा 25

इन संख्याओं का महत्तम समापवर्तक = 25
अभीष्ट लघुत्तम समापवर्त्य = 25/1000
लघुत्तम समापवर्त्य = 0.025

महत्वपूर्ण बिन्दु :-

1. अपवर्त्य या गुणज (Multiple) :- किसी संख्या का अपवर्त्य वे सभी संख्याएँ होती हैं जिसमें उस संख्या से पूर्ण भाग किया जाता हैं।

जैसे :-

3 का अपवर्त्य = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
4 का अपवर्त्य = 4, 8, 12, 16, 20, 24, 27, 32, 36, 40

2. अपवर्तक या गुणनखण्ड (Factor) :- किसी संख्या का अपवर्तक वे सभी संख्याएँ हैं जो उस संख्या को पूर्णतः विभाजित कर देती हैं।

जैसे :-

42 का अपवर्तक = 1, 2, 3, 6, 7, 14, 21, 42
48 का अपवर्तक = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48

3. सह-अभाज्य संख्या (Co-Prime Number) :- ऐसी दो संख्याएँ x और y सह अभाज्य संख्या कहलाती हैं। जिनका महत्तम समापवर्तक 1 हो।

जैसे :- (5, 9), (7, 11), (2, 7) आदि सह-अभाज्य संख्याओं के जोड़े हैं।

लघुत्तम समापवर्त्य और महत्तम समापवर्तक के सूत्र

• L.C.M × H.C.F = प्रथम संख्या × द्धितीय संख्या
• LCM = अंशों का लघुत्तम समापवर्त्य / हर का महत्तम समापवर्तक
• HCF = अंशों का महत्तम समावतर्क / हर का लघुत्तम समापवर्तक
• भिन्नों का लघुत्तम समापवर्तक (L.C.M.) = अंशों का लघुत्तम समापवर्त्य / हर का महत्तम समापवर्तक
• भिन्नों महत्तम समावतर्क (H.C.F.) = अंशों का महत्तम समापवर्तक / हर का लघुत्तम समापवर्त्य

लघुत्तम समापवर्त्य पर आधारित प्रश्न

Q.1 12, 24, 48 का गुणनखण्ड विधि से लघुत्तम समापवर्त्य निकालिए?
A. 12
B. 28
C. 36
D. 48

हल:- प्रश्नानुसार,
12 = 2 × 2 × 3
24 = 2 × 2 × 2 × 3
48 = 2 × 2 × 2 × 2 × 3
L.C.M. = 2 × 2 × 2 × 2 × 3
L.C.M. = 48
Ans. 48

Q.2 15, 30, 60 का गुणनखण्ड विधि से लघुत्तम समापवर्त्य निकालिए?
A. 12
B. 28
C. 36
D. 60

हल:- प्रश्नानुसार,
15 = 3 × 5
30 = 2 × 3 × 5
60 = 2 × 2 × 3 × 5
L.C.M. = 2 × 2 × 3 × 5
L.C.M. = 15 × 4
L.C.M. = 60
Ans. 60

Q.3 16, 64, 128 का गुणनखण्ड विधि से लघुत्तम समापवर्त्य निकालिए?
A. 16
B. 32
C. 64
D. 128

हल:- प्रश्नानुसार,
16 = 2 × 2 × 2 × 2
64 = 2 × 2 × 2 × 2 × 2 × 2
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
L.C.M. = 2 × 2 × 2 × 2 × 2 × 2 × 2
L.C.M. = 128
Ans. 128

Q.4 24, 36, 40 का LCM निकालिए?
A. 430
B. 360
C. 420
D. 520

हल:- प्रश्ननानुसार,
24, 36, 40 का महत्तम समापवर्तक
24 = 2 × 2 × 2 × 3
36 = 2 × 2 × 3 × 3
40 = 2 × 2 × 2 × 5
LCM = 2 × 2 × 2 × 3 × 3 × 5
LCM = 360
Ans. 360

Q.5 66, 75, 130 का लघुत्तम समापवर्तक निकालिए?
A. 20450
B. 21450
C. 22450
D. 23450

हल:- प्रश्नानुसार,
66, 75, 130 का लघुत्तम समापवर्तक
66 = 2 × 3 × 11
75 = 3 × 5 × 5
130 = 2 × 5 × 13
लघुत्तम समापवर्तक = 2 × 3 × 5 × 5 × 11 × 13
लघुत्तम समापवर्तक = 21450
Ans. 21450

Q.6 9, 30, 27, 15 का लघुत्तम समापवर्तक ज्ञात कीजिए?
A. 270
B. 240
C. 320
D. 120

हल:- प्रश्नानुसार,
9, 30, 27, 15 का लघुत्तम समापवर्तक
9 = 3 × 3
30 = 2 × 3 × 5
27 = 3 × 3 × 3
15 = 3 × 5
अभीष्ट लघुत्तम समापवर्तक = 2 × 3 × 3 × 3 × 5
लघुत्तम समापवर्तक = 270
Ans. 270

Q.7 36 और 84 का लघुत्तम समापवर्तक ज्ञात कीजिए?
A. 270
B. 242
C. 252
D. 320

36 = 2 × 2 × 3 × 3
84 = 2 × 2 × 3 × 3 × 7
अभीष्ट लघुत्तम समापवर्तक = 2 × 2 × 3 × 3 × 7
लघुत्तम समापवर्तक = 252
Ans. 252

Q.8 3/4, 6/7, 8/9 का लघुत्तम समापवर्तक ज्ञात कीजिए?
A. 24
B. 3
C. 3/56
D. 8

हल:- प्रश्नानुसार,
3/4, 6/7, 8/9 का लघुत्तम समापवर्तक
भिन्नों का लघुत्तम समापवर्तक (L.C.M.) = अंशों का लघुत्तम समावतर्क / हर का महत्तम समावतर्क
लघुत्तम समापवर्तक = (3, 6, और 8 का ल. स.)/(4, 6, और 7 का म. स.)
लघुत्तम समापवर्तक = 24/1
लघुत्तम समापवर्तक = 24
Ans. 24

Q.8 5/7, 7/8 एवं 8/9 का लघुत्तम समापवर्तक हैं?
A. 120
B. 280
C. 360
D. 480

हल:- प्रश्नानुसार,
5/7, 7/8 एवं 8/9 का लघुत्तम समापवर्तक
भिन्नों का लघुत्तम समापवर्तक (L.C.M.) = अंशों का लघुत्तम समावतर्क / हर का महत्तम समावतर्क
लघुत्तम समापवर्तक (L.C.M.) = (5, 7, 8 का ल. स.)/(7,8,9 का म.स.)
लघुत्तम समापवर्तक (L.C.M.) = 280
Ans. 280

Q.9 1/3, 5/6, 2/9, 4/27 का लघुत्तम समापवर्तक हैं?
A. 10/27
B. 20/3
C. 20/27
D. 1/54

हल:- प्रश्नानुसार,
1/3, 5/6, 2/9, 4/27 का लघुत्तम समापवर्तक
भिन्नों का लघुत्तम समापवर्तक (L.C.M.) = अंशों का लघुत्तम समावतर्क / हर का महत्तम समावतर्क
अभीष्ट ल.स. = 1, 5, 2 तथा 4 का ल.स./3, 6, 9 तथा 27 का म.स.
अभीष्ट ल.स. = 20/3
Ans. 20/3

Q.10 छोटे से छोटा वह भिन्न जो 6/7, 5/14, 10/21 से पुर्णतः विभक्त हो जाए हैं?
A. 30/98
B. 60/90
C. 30/7
D. 60/147

हल:- प्रश्नानुसार,
भिन्नों का लघुत्तम समापवर्तक (L.C.M.) = अंशों का लघुत्तम समावतर्क / हर का महत्तम समावतर्क
अभीष्ट ल. स. = (6,5,10 का ल. स.)/(7,14,21 का म.स.)
30/7
Ans. 30/7

Q.11 0.9, 0.18, 3.6, 7.2, 0.144 का लघुत्तम समापवर्तक क्या हैं?
A. 1.44
B. 7.2
C. 12.96
D. 18.32

हल:- प्रश्नानुसार,
0.9, 0.18, 3.6, 7.2, 0.144
दशमलव के बाद अधिकतम तीन अंक हैं।
इसलिए सभी संख्याओं को 1000 से गुणा करने पर प्राप्त संख्या
= 900, 180, 3600, 7200 तथा 144
इन संख्याओं का ल. स. = 7200
अभीष्ट ल. स. = 7200/100
लघुत्तम समापवर्तक = 7.2
Ans. 7.2

Q.12 x² + xy + y² और x³ – y³ का L.C. M. होगा?
A. x – y
B. x² – y²
C. x³ – y³
D. x² + xy + y²

हल:- प्रश्नानुसार,
x² + xy + y² =
x³ – y³ = (x – y)(x² + xy + y²)
अभीष्ट L.C.M. = (x – y) (x² + xy + y² )
Ans. x³ – y³

Q.13 4⁷, 4⁵, 4⁶, 4⁴, L.C.M. ज्ञात कीजिए?
A. 4⁵
B. 4⁷
C. 4⁶
D. 4⁴

हल:- सभी संख्याओं का आधार 4 हैं। तथा अधिकतम घात 4⁷ का हैं।
लघुत्तम समापवर्त्य = 5¹²
Ans. 4⁷

Q.14 10 a²bc, 15 abc², 20 a²b²c का लघुत्तम समापवर्तक क्या हैं?
A. 60a²b²c²
B. 40ab²c²
C. 70a²b²c
D. 90abc²

हल:- प्रश्नानुसार,
10 a²bc = 5×2×a²×b×c
15 abc²= 5×3×a×b×c²
20 a²b²c = 5×2²×a²×b²×c
L.C.M. = 5×2²×3×a²×b×c
L.C.M. = 60a²b²c²
Ans. 60a²b²c²

Q.15 8(x³−x) और 4(x³ −1) का लघुत्तम समापवर्तक होगा?
A. 4 (x²−1)(x+1)
B. 8x (x²−1)(x²+x+1)
C. 4 (x²−1)
D. 8(x²−1)(x²+x+3)

हल:- प्रश्नानुसार,
8(x³−x) = 2³ × x × (x – 1)(x + 1)
4(x³ −1) = 2² × (x – 1)(x² + x + 1)
लघुत्तम समापवर्तक = 2³ × x × (x – 1)(x + 1) (x² + x + 1)
लघुत्तम समापवर्तक = 8x (x – 1)(x² + x + 1)

महत्तम समापवर्तक पर आधारित प्रश्न

Q.16 18, 42, 102 का महत्तम समापवर्तक निकालिए?
A. 12
B. 2
C. 6
D. 8

हल:- प्रश्नानुसार,
18 = 2 × 3 × 3
42 = 2 × 3 × 7
102 = 2 × 3 × 17
उभयनिष्ठ अभाज्य गुणनखंड 2 और 3 हैं।
अभीष्ट महत्तम समापवर्तक = 2 × 3
HCF = 6
Ans. 6

Q.17 60, 45, 180, 24, का HCF निकालिये?
A. 2
B. 3
C. 5
D. 8

हल:- प्रश्नानुसार,
60 = 2 × 2 × 3 × 5
45 = 3 × 3 × 5
180 = 2 × 2 × 3 × 3 × 5
24 = 2 × 2 × 2 × 3
उभयनिष्ठ अभाज्य गुणनखंड 3 हैं।
अभीष्ट महत्तम समापवर्तक = 3
Ans. 3

Q.18 923, 949 का HCF निकालिए?
A. 12
B. 13
C. 16
D. 18

हल:- प्रश्नानुसार,
923 = 13 × 71
949 = 13 × 73
उभयनिष्ठ अभाज्य गुणनखंड 13 हैं।
अभीष्ट महत्तम समापवर्तक = 13
Ans. 13

Q.19 36 और 84 का महत्तम समापवर्तक ज्ञात कीजिए?
A. 4
B. 6
C. 12
D. 18

हल:- प्रश्नानुसार,
36 और 84 का महत्तम समापवर्तक
36 = 2 × 2 × 3 × 3
84 = 2 × 2 × 3 × 7
उभयनिष्ठ अभाज्य गुणनखंड 2 तथा 3 हैं।
अभीष्ट म.स. = 2 × 2 × 3
अभीष्ट म.स. = 12
Ans. 12

Q.20 216, 288 और 720 का महत्तम समापवर्तक ज्ञात कीजिए?
A. 120
B. 280
C. 360
D. 480

हल:- प्रश्नानुसार,
216 = 2 × 2 × 2 × 3 × 3 × 3
288 = 2 × 2 × 2 × 2 × 2 × 3 × 3
720 = 2 × 2 × 2 × 2 × 3 × 3 × 5
उभयनिष्ठ अभाज्य गुणनखंड 2 और 3 हैं।
अभीष्ट महत्तम समापवर्तक = (2 × 2 × 2 × 3 × 3)
महत्तम समापवर्तक = 72
Ans. 72

Q.21 9/10, 12/25, 18/35, 21/40 का महत्तम समापवर्तक निकालिए?
A. 12/700
B. 28/3200
C. 6/1400
D. 48/4800

हल:- HCF = 9, 12, 18, 21
= 2 × 3
= 6
LCM = 2 × 2 × 2 × 5 × 5 × 7
LCM = 1400
HCF = अंश का महत्तम समावतर्क / हर का लघुत्तम समावतर्क
HCF = 6/1400
Ans. 6/1400

Q.22 x² – 9 और x² – 6x + 9 का महत्तम समापवर्तक हैं?
A. x – 3
B. x + 3
C. x + 2
D. x – 2

हल:- प्रश्नानुसार,
x² – 9 = (x – 3)(x – 3)
x² – 6x + 9 = x² – 3x – 3x + 9
x(x – 3) – 3(x- 3)
(x – 3)(x – 3)
अभीष्ट महत्तम समापवर्तक = (x – 3)
Ans. (x – 3)

Q.23 2.4, 0.36 और 7.2 का महत्तम समापवर्तक ज्ञात कीजिए?
A. 12
B. 120
C. 1.2
D. 0.12

हल:- प्रश्नानुसार,
2.4, 0.36, 7.2
दशमलव के बाद अधिकतम दो अंक हैं।
इसलिए सभी संख्याओं को 100 से गुणा करने पर प्राप्त
संख्या = 240, 36, तथा 720
इन संख्याओं का ल. स. = 12
अभीष्ट ल. स. = 12/100
लघुत्तम समापवर्तक = 0.12
Ans. 0.12

Q.24 7⁸, 7⁶, 7⁵, 7¹⁰ महत्तम समापवर्तक ज्ञात कीजिए?
A. 7⁸
B. 7⁷
C. 7⁵
D. 7¹⁰

हल:- सभी संख्याओं का आधार 7 हैं। तथा सबसे छोटी घात 7⁵ का हैं।
लघुत्तम समापवर्त्य = 7⁵
Ans. 7⁵

Q.25 2.4, 0.36 तथा 7.2 का महत्तम समापवर्तक ज्ञात कीजिए?
A. 12
B. 120
C. 12.9
D. 15.7

हल:- प्रश्नानुसार,
चूंकि दशमलव के बाद अधिकतम दो अंक हैं,
इसलिए सभी संख्याओं को 100 से गुणा करने पर प्राप्त संख्या = 240, 36 तथा 720 होंगे।
240 = 2 × 2 × 2 × 2 × 3 × 5
36 = 2 × 2 × 3 × 3
720 = 2 × 2 × 2 × 2 × 3 × 3 × 5
240, 36, 720 का म.स. = 2 × 2 3
240, 36, 720 का म.स. = 12
अभीष्ट म.स. = 12/100
अभीष्ट म.स. = 0.12
Ans. 0.12

Q.26 यदि (x – a), (x² – x – 6) और (x² + 3x – 18) का महत्तम समापवर्तक हैं, तो a का मान होगा?
A. 2
B. 4
C. 6
D. 8

हल:- प्रश्नानुसार,
(x² – x – 6) = (x² – x – 6)
(x² – x – 6) = x² – 3x + 2x – 6
(x² – x – 6) = x(x – 3) + 2(x – 3)
(x² – x – 6) = (x – 3)(x + 3)
(x² + 3x – 18) = (x² + 3x – 18)
(x² + 3x – 18) = x² + 6x – 3x – 18
(x² + 3x – 18) = x (x + 6) – 3(x + 6)
(x² + 3x – 18) = (x – 3)(x + 6)
म.स. = 1 = (x – 3)
म.स. = 1 = (x – a)
x – 3 = x – a
x – x – a = – 3
– a = – 3
a = 3
Ans. 3

Q.27 1295/1591 को जब निम्नतम पद में से घटाया जाए तो संख्या प्राप्त होगी?
A. 35/37
B. 37/43
C. 35/43
D. 43/35

हल:- प्रश्नानुसार,
1295 और 1591 महत्तम समापवर्तक = 37
(1295÷37)/(1591÷37)
Ans. 35/43

Q.28 a²−1, a³−1 और 8a³−8a का महत्तम समापवर्तक हैं?
A. a + 1
B. a – 1
C. a² + 1
D. a² – 1

हल:- प्रश्नानुसार,
a²−1 = (a + 1)(a – 1)
a³−1 = (a – 1)(a² + a +1)
8a³−8a = 8a (a -1)(a² + a +1)
महत्तम समापवर्तक = (a – 1)
Ans. a – 1

लघुत्तम समापवर्त्य और महत्तम समापवर्तक पर आधारित प्रश्न

Q.1 दो संख्याओं x एवं y का लघुत्तम समापवर्त्य a हैं x तथा y का महत्तम समापवर्तक होगा?
A. xy
B. a/xy
C. xy/a
D. ax/y

हल:- प्रश्नानुसार,
महत्तम समापवर्तक = (दोनों संख्याओं का गुणनफल)/(लघुत्तम समापवर्त्य)
महत्तम समापवर्तक = xy/a

Q.2 368/437 का सरलतम रूप क्या है?
A. 12/17
B. 16/19
C. 9/14
D. 18/23

हल:- प्रश्नानुसार,
HCF = 23
368 / 23 = 16
437 / 23 = 19
सरलतम रूप 16/19 होगा।
Ans. 16/19

Q.3 वह छोटी से छोटी संख्या कौन सी हैं, जो 4, 6, 8, 9, 12, से पूर्णतः विभाजित हो?
A. 18
B. 32
C. 68
D. 72

हल:- 4, 6, 8, 9, 12, का LCM = 72
अतः वह छोटी से छोटी संख्या 72 होंगी।
Ans. 72

Q.4 5⁻¹¹, 5⁻⁹, 5⁻¹⁶, 5⁻¹⁰ का लघुत्तम समावतर्क एवं महत्तम समावतर्क निकालिए?
A. 5⁻¹⁶
B. 5⁻¹¹
C. 5⁻⁹
D. 5⁻¹⁰

हल:- प्रश्ननानुसार,
सभी संख्याओं का आधार 5 हैं
तथा -9 > -10 > -11 > -16
LCM = 5⁻⁹
HCF = 5⁻¹⁶
Ans. 5⁻¹⁶

Q.5 दो संख्याओं के L.C.M. और H.C.F. क्रमशः 48, 8, हैं यदि इनमे से एक संख्या 24 हैं, तो दूसरी संख्या क्या होगी?
A. 16
B. 8
C. 32
D. 18

हल:- प्रश्ननानुसार,
L.C.M × H.C.F = प्रथम संख्या × द्धितीय संख्या
24 × X = 48 × 8
X = 48 × 8 / 24
X = 16
Ans. 16

Q.6 दो संख्याओं का L.C.M. 1920 तथा H.C.F. 16 हैं, यदि इनमें से एक संख्या 128 हो तो दूसरी संख्या क्या होगी?
A. 160
B. 832
C. 240
D. 512

हल:- प्रश्ननानुसार,
माना, दूसरी संख्या = x
L.C.M × H.C.F = प्रथम संख्या × द्धितीय संख्या
x × 128 = 1920 × 16
x = 1920 × 16/128
x = 240
अतः दूसरी संख्या = 240
Ans. 240

Q.7 वह छोटी से छोटी संख्या कौन सी हैं जिसे 14, 21, 28, 35 से विभाजित करने पर प्रत्येक स्थिति में 5 शेष बचे?
A. 165
B. 285
C. 425
D. 350

हल:- प्रश्ननानुसार,
14, 21, 28, 35 का LCM = 420
420 + 5 = 425
Ans. 425

Q.8 a,b,c एक वृताकार स्टेडियम में उसके चारों और एक ही बिंदु से एक साथ दौड़ना प्रारंभ करते हैं तथा क्रमशः 28, 24, 32 सेकण्ड में एक चक्कर पूरा करते हैं वे तीनों कितने समय बाद प्रारम्भिक बिंदु पर फिर से मिलेंगे?
A. 16/5
B. 8/3
C. 24/5
D. 3/7

हल:- प्रश्ननानुसार,
L.C.M. = 288
288/60
24/5
Ans. 24/5

Q.9 तीन विभिन्न चौराहों पर आवागमन सूचक वृतिया क्रमशः 48 सेकेण्ड, 72 सेकेंड, और 108 सेकेंड के बाद बदलती हैं यदि वे एक साथ अभी बदली हो तो फिर कितने समय बाद बदलेगी?
A. 165
B. 285
C. 432
D. 350

हल:- प्रश्ननानुसार,
48, 72, 108 का L.C.M. = 432
Ans. 432

Q.10 3 प्रकार के तारों की लंबाई क्रमशः 4672, 3869, 2993, मीटर हैं, एक अन्य प्रकार के तार की अधिकतम लम्बाई क्या है जिससे तीनों प्रकार के तारों की लंबाई को पूर्णतः नापा जा सकें।
A. 16
B. 28
C. 43
D. 73

हल:- प्रश्ननानुसार,
4672, 3869, 2993 का HCF = 73
Ans. 73

Q.11 दो संख्याओं का लासा 495 है तथा उनका महत्तम समापवर्तक 5 है यदि उन संख्याओं का योग 100 हो तो उन का अंतर कितना होगा?
A. 5
B. 10
C. 15
D. 20

हल:- प्रश्ननानुसार,
माना की पहली संख्या = a
दूसरी संख्या = b
सूत्र – प्रथम संख्या × दूसरी संख्या = ल.स × म.स
a × b = 495 × 5
ab = 2475
प्रश्ननानुसार,
a + b = 100
सूत्र – (a – b)² = ( a + b )² – 4ab
(100)² – 4 × 2475
10000 – 9900
(a – b)² = 100
(a – b) = √100
(a – b) = 10
Ans. 10

Q.12 वह बड़ी से बड़ी संख्या ज्ञात कीजिए जिससे 29 30 और 3250 में भाग देने पर क्रमशः 7 और 11 शेष बचे?
A. 79
B. 59
C. 89
D. 69

हल:- प्रश्ननानुसार,
2930 – 7 = 2923 और
3250 – 11 = 3239
इसीलिए 2923 और 3239 का म.स.प. = 79
इसीलिए वह संख्या 79 हैं।
Ans. 79

Q.13 वह छोटी से छोटी संख्या निकालें जिसे 5, 6, 7, 8 से भाग देने पर 3 शेष बचता है परन्तु 9 से भाग देने पर कोई शेष नही बचता?
A. 1560
B. 1683
C. 1820
D. 1960

हल :- प्रश्ननानुसार,
5, 6, 7, 8 का ल.स. = 840
अतः वाँछित संख्या = (840 × n + 3) होगी।
जहाँ n कोई प्राकृत संख्या हैं।
n का न्यूनतम मान, जिससे (840 × n + 3), 9 से विभाज्य हो,
वह न्यूनतम मान n = 2 होगा।
अभीष्ट संख्या = 840 × 2 + 3
अभीष्ट संख्या = 1683
Ans. 1683

Q.14 वह छोटी से छोटी संख्या ज्ञात करें जो 10, 20, 30, 40 तथा 50 से भाग देने पर प्रत्येक दशा में 7 शेष बचे?
A. 607
B. 709
C. 504
D. 810

हल:- प्रश्ननानुसार,
सूत्र :- वह छोटी से छोटी संख्या बताये जो x, y, z तथा p से भाग देने पर प्रत्येक दशा में सामान शेष (k) बचे तो संख्या = ल.स. (x, y, z, p) + k )
अभीष्ट संख्या = ल.स. (10, 20, 30, 40, 50) + 7
= 600 + 7
= 607
Ans. 607

Q.15 चार अंक की सबसे छोटी संख्या ज्ञात करे जो 2, 3, 4, 5, 6 और 7 से पूर्ण रूप से भाज्य हो?
A. 1270
B. 1260
C. 1570
D. 1470

हल:- प्रश्ननानुसार,
सबसे पहले हम 2, 3, 4, 5, 6 और 7 का ल.स. निकालेंगे
ल.स. (2, 3, 4, 5, 6 और 7) = 420
चूँकि हमें 4 अंक की संख्या चाहिए अतः अभीष्ट संख्या अवश्य ही 420 का गुणक होगा.
अभीष्ट संख्या = 420 x 3
अभीष्ट संख्या = 1260
Ans. 1260

Q.16 दो संख्याओं का गुणनफल 7168 है एवं उनका म0 स0 16 है तो संख्याएं क्या है?
A. 111, 11
B. 124, 13
C. 132, 7
D. 112, 64

हल:- प्रश्ननानुसार,
माना कि संख्याएं 16a तथा 16b हैं तथा परस्पर अभाज्य भी हैं
अत: 16a x 16b = 7168
= 28
अब वे जोडे देखते हैं जिनका गुणनफल 28 होता है
वे हैं (28,1) तथा (7,4)
अत: संख्याएं हो सकती हैं (448 , 16)
तथा (112 , 64)
Ans. 112, 64

Q.17 दो व्यजकों का महत्तम समापवर्तक (x + 2) और लघुत्तम समापवर्तक (x + 2) (x – 1) (x² – 2x + 4) हैं यदि उनमें से एक व्यंजक (x² – 2x + 4) हो, तो दूसरा व्यंजक होगा?
A. (x + 2)
B. (x – 1)
C. (x + 2)(x – 1)
D. (x + 2)² (x – 1)

हल:- प्रश्नानुसार,
दूसरा व्यंजक = (ल.स.× म.स.)/प्रथम व्यंजक
[(x + 2)(x – 1)(x² – 2x + 4) × (x + 2)]/(x² – 2x + 4)
(x + 2)(x – 1)(x + 2)
(x + 2)² (x – 1)
Ans. (x + 2)² (x – 1)

Q.18 दो संख्याओं का म. स. 16 तथा ल. स. 160 हैं यदि इनमें से एक संख्या 32 हो, तो दूसरी संख्या होंगी?
A. 48
B. 80
C. 96
D. 112

हल:- प्रश्नानुसार,
दूसरी संख्या = (ल.स.× म.स.)/पहली संख्या
दूसरी संख्या = (16 × 160)/32
दूसरी संख्या = 80
Ans. 80

Q.19 दो संख्याओं का ल. स. 225 हैं तथा उनका म. स. 5 हैं यदि एक संख्या 25 हो, तो दूसरी संख्या होगी?
A. 5
B. 45
C. 35
D. 225

हल:- प्रश्नानुसार,
दूसरी संख्या = (ल.स.× म.स.)/पहली संख्या
दूसरी संख्या = (225 × 5)/25
दूसरी संख्या = 9 × 5
दूसरी संख्या = 45
Ans. 45

Q.20 दो संख्याओं का ल. स 864 हैं और उनका म. स 144 हैं यदि उनमें से एक संख्या 288 हो, तो दूसरी संख्या होंगी?
A. 567
B. 255
C. 432
D. 225

हल:- प्रश्नानुसार,
दूसरी संख्या = (ल.स.× म.स.)/पहली संख्या
दूसरी संख्या = (864 × 144)/288
दूसरी संख्या = 144 × 3
दूसरी संख्या = 432
Ans. 432

Q.21 13 का वह सबसे छोटा गुणज जिसे 4, 5, 6, 7 और 8 से भाग देने पर प्रत्येक स्थिति में 2 शेष बचें?
A. 2522
B. 2552
C. 4323
D. 2225

हल:- प्रश्नानुसार,
4, 5, 6, 7 और 8 लघुत्तम समापवर्तक = 840
संख्या = (840 × n + 2), होगी।
जहाँ n कोई प्राकृतिक संख्या हैं।
n का न्यूनतम मान जिससे (840 × n + 2), 13 से विभाज्य हो।
न्यूनतम मान n = 3 होगा।
अभीष्ट संख्या = 840 × 3 + 2
अभीष्ट संख्या = 2520 + 2
अभीष्ट संख्या = 2,522
Ans. 2,522

Q.22 तीन विभिन्न चौराहों पर आवागमन सूचक बत्तियाँ क्रमशः 48 सेकेण्ड, 72 सेकेंड, और 108 सेकेंड के बाद बदलती हैं यदि वे 8 :20 : 00 बजे बदली हो तो फिर कितने समय बाद बदलेगी?
A. 8 : 27 : 27
B. 8 : 27 : 32
C. 8 : 27 : 12
D. 8 : 27 : 18

हल:- प्रश्नानुसार,
पुनः बत्तियों का साथ बदलने का समय
48, 72, और 108 का L.C.M. = 432
अर्थात 7 मिनिट 12 सेकेण्ड
पुनः बत्तियाँ बदलने में परिवर्तन होगा = 8 : 27 : 12
Ans. 8 : 27 : 12

Q.23 एक मंदिर में 6 घण्टियाँ लगी हुई हैं, जिनमें से वे क्रमशः 4 सेकेण्ड, 6 सेकेण्ड, 8 सेकेण्ड, 20 सेकेण्ड, और 12 सेकेंड और 18 सेकेण्ड में बजती हैं यदि वे एक साथ अभी बजी हो तो फिर कितने समय बाद बजेगी?
A. 120
B. 140
C. 180
D. 220

हल:- प्रश्नानुसार,
एक मंदिर में घण्टियाँ लगी हैं = 6
4, 6, 8, 20, 12, 18 का L.C.M. = 180
अतः 180 सेकेण्ड के बाद पुनः मंदिर में घण्टियाँ बजेगी।

Q.24 एक मंदिर में 6 घण्टियाँ लगी हुई हैं, जिनमें से वे क्रमशः 10 सेकेण्ड, 12 सेकेण्ड, 15 सेकेण्ड, 20 सेकेण्ड, और 25 सेकेंड और 30 के अंतराल पर बजती हैं यदि वे एक साथ अभी  बजी हो तो फिर कितने समय बाद बजेगी?
A. 150
B. 200
C. 250
D. 300

हल:- प्रश्नानुसार,
एक मंदिर में घण्टियाँ लगी हैं = 6
10, 12, 15, 20, 25, 30 का L.C.M. = 300
अतः 300 सेकेण्ड के बाद पुनः मंदिर में घण्टियाँ बजेगी।

FAQ

जरूर पढ़िए :

• सरलीकरण
• दशमलव भिन्न
• BODMAS का नियम
• आरोही क्रम और अवरोही क्रम

उम्मीद हैं आपको लघुत्तम समापवर्त्य और महत्तम समापवर्तक की पोस्ट पसंद आयी होगीं।

यदि आपको लघुत्तम समापवर्त्य और महत्तम समापवर्तक की ये पोस्ट पसंद आयी हो तो अपने दोस्तों के साथ जरूर शेयर करें।

यदि आप लघुत्तम समापवर्त्य और महत्तम समापवर्तक से सम्बन्धित कुछ प्रश्न पूछना चाहते हैं तो कमेंट में जरूर पूछें धन्यवाद।