समलम्ब चतुर्भुज की परिभाषा इसके सूत्र, प्रकार और उदाहरण

इस पेज पर हम समलंब चतुर्भुज की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।

पिछले पेज पर हमने आयत और वर्ग की जानकारी शेयर की हैं तो उन पोस्टों को भी पढ़े।

चलिए आज हम समलंब चतुर्भुज किसे कहते हैं इसके सूत्र, प्रकार और उदाहरण की समस्त जानकारी को पढ़ते और समझते हैं।

Table of Contents

समलम्ब चतुर्भुज की परिभाषा

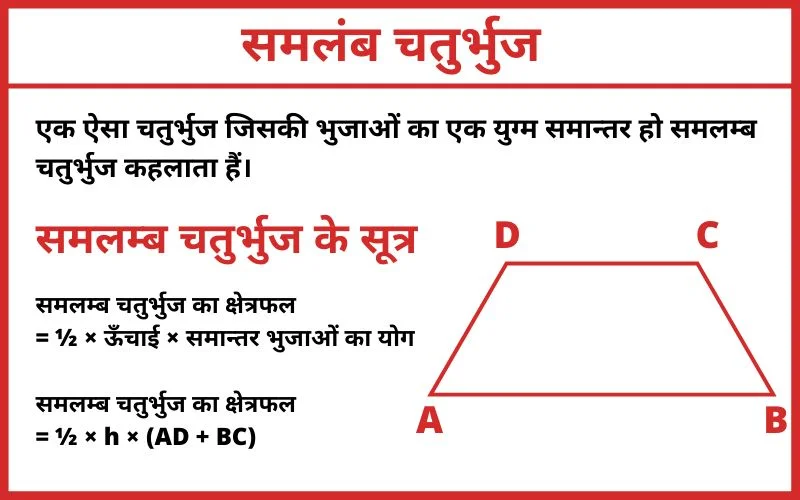
एक ऐसा चतुर्भुज जिसकी भुजाओं का एक युग्म समान्तर हो समलम्ब चतुर्भुज कहलाता हैं।

दूसरें शब्दों में ऐसी चार भुजाओं वाली एक ज्यामितीय आकृति जिसकी कोई दो सम्मुख भुजाएँ समान्तर हो लेकिन दो तिर्यक भुजाएँ असमान हो समलम्ब चतुर्भुज कहलाता हैं।

सरल शब्दों में, जिस चतुर्भुज की सम्मुख भुजाओं का केवल एक युग्म समान्तर हो, उसे समलम्ब चतुर्भुज कहते हैं।

गणितज्ञों के अनुसार, समलम्ब एक ऐसा चतुर्भुज है जिसमें दो समानांतर भुजाएँ होती हैं समलम्ब चतुर्भुज के समानांतर भुजाओं को आधार तथा असमानांतर भुजाओं को Legs कहा जाता हैं।

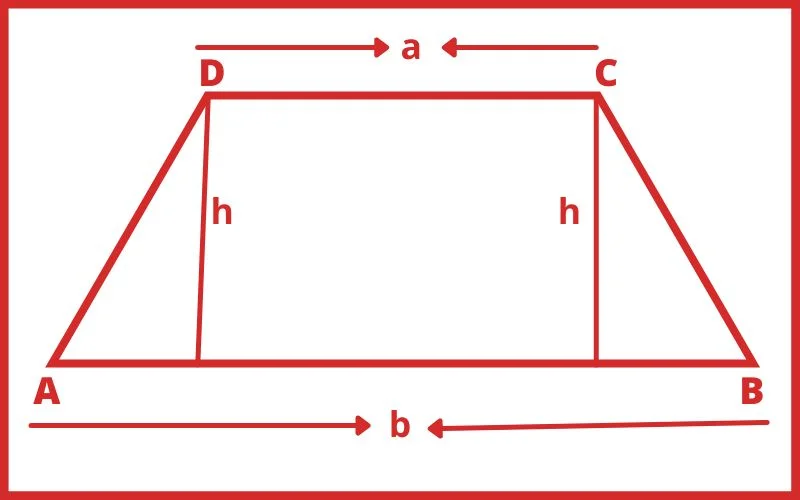
समलम्ब चतुर्भज में, AD || BC तथा दूसरे में, AB और CD एक दूसरे के समानांतर हैं जबकि AC और BD असमानांतर हैं। साथ ही h दो समानांतर भुजाओं के बीच की दूरी है जो समलम्ब चतुर्भुज की ऊंचाई हैं।

चारों अंतः कोण का योग 360 डिग्री होता हैं।

अर्थात ∠A + ∠B + ∠C + ∠D = 360

समलम्ब चतुर्भुज के सूत्र

समलम्ब चतुर्भुज का क्षेत्रफल = ½ × ऊँचाई × समान्तर भुजाओं का योग
समलम्ब चतुर्भुज का क्षेत्रफल = ½ × h × (AD + BC)

समलम्ब चतुर्भुज के प्रकार

समलम्ब चतुर्भुज को तीन भागों में बाटाँ गया हैं।

1. समद्विबाहु समलम्ब चतुर्भुज

इस चतुर्भुज में असमान्तर भुजाएँ सामान लम्बाई की होती हैं जिसे समद्विबाहु चतुर्भुज कहा जाता हैं।

2. विषम समलम्ब चतुर्भुज

ऐसा चतुर्भुज जिसमें भुजाओं एवं कोणों का माप अलग-अलग हो, वह विषम भुजा एवं कोण वाला समलम्ब चतुर्भुज कहलाता हैं।

3. समकोण समलम्ब चतुर्भुज

ऐसा चतुर्भुज जिसमें कम-से कम दो समकोण अवश्य हो समकोण समलम्ब चतुर्भुज कहलाता हैं।

समलम्ब चतुर्भुज की विशेषताएँ

समलम्ब चतुर्भुज में चार भुजाएँ एवं चार शीर्ष होते हैं।
समलम्ब चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
समांतर भुजा समद्विबाहु समलम्बाकार चतुर्भुज को छोड़कर असमान हैं।
इस चतुर्भुज के सम्मुख भुजा का केवल एक युग्म समान्तर होता है तथा शेष युग्म तिर्यक होते हैं।
असामान्तर भुजाओं के मध्य बिन्दुओं को मिलनेवाली रेखाखंड की लम्बाई समानान्तर भुजाओं के लम्बाई का योग होता हैं।
दो समान्तर भुजाओं के बीच दोनों से समान दूरी पर खींची गयी सरल रेखा इन दोनों भुजाओं के समान्तर माध्य के बराबर होती हैं।

उदाहरण 1. एक समलंब की दो समांतर भुजाओं की लंबाई 3: 2 के अनुपात में दी गई है और उनके बीच की दूरी 8 सेमी है। यदि समलंब का क्षेत्रफल 400 वर्ग सेमी है, तो समांतर भुजाओं की लंबाई ज्ञात करें?

हल : माना कि, 2 समांतर भुजा 3x और 2x दी गई हैं।
तो समलंब का क्षेत्रफल = ¹/₂ x समांतर भुजाओं के बीच की दूरी x समांतर भुजाओं का योगफल
400 = ¹/₂ x (3x + 2x) x 8
400 = ¹/₂ x 5x x 8
400 = 20x
x = 20 सेमी

समांतर भुजाओं की लंबाई 60 सेमी और 40 सेमी है।

उदाहरण 2. एक समलंब की दो समांतर भुजाएँ की लम्बाई क्रमशः 27 सेमी और 19 सेमी हैं, और उनके बीच की दूरी 14 सेमी है। समलंब का क्षेत्रफल ज्ञात कीजिए?

हल : प्रश्नानुसार,
समलंब का क्षेत्रफल = ¹/₂ x समांतर भुजाओं के बीच की दूरी x समांतर भुजाओं का योगफल
समलंब का क्षेत्रफल = [¹/₂ × (27 + 19) × 14] cm² = 322 सेमी²

उदाहरण 3. एक समलंब का क्षेत्रफल 352 सेमी² है और इसकी समांतर भुजाओं के बीच की दूरी 16 सेमी है। यदि समांतर भुजा में से एक की लंबाई 25 सेमी है, तो दूसरी भुजा की लंबाई ज्ञात करें।

हल : मान लीजिए अभीष्ट भुजा की लंबाई x सेमी है।
तो समलंब का क्षेत्रफल= {¹/₂ × (25 + x) × 16} सेमी²
समलंब का क्षेत्रफल = (200 + 8x) सेमी².
लेकिन समलंब का क्षेत्रफल = 352 सेमी² (दिया गया है)
अतः, 200 + 8x = 352
⇒ 8x = (352 – 200)
⇒ 8x = 152
⇒ x = (152/8)
⇒ x = 19
दूसरे भुजा की लंबाई 19 सेमी है।

उदाहरण 4. एक समलंब का क्षेत्रफल क्या है जब आधार क्रमशः 12 सेमी और 20 सेमी हैं और दो समानांतर भुजाओं के बीच की दूरी 10 सेमी है?

हल : दिया गया है,
a = 12 सेमी
b = 20 सेमी
दो समान्तर भुजाओं के बीच की दूरी h = 10 सेमी
समलम्ब चतुर्भुज का क्षेत्रफल = 1/2 (12 + 20) 10
= 160 सेमी²

FAQ

Q.1 समलंब चतुर्भुज का अर्थ क्या है?

Ans. समलंब चतुर्भुज एक चतुर्भुज है जिसमें दो समानांतर भुजाएँ और दो गैर-समानांतर भुजाएँ होती हैं।

Q.2 समलंब चतुर्भुज का गुण क्या है?

Ans. समलम्ब चतुर्भुज समानांतर भुजाएँ वर्गों और आयतों से भी भिन्न होती हैं क्योंकि वर्गों और आयतों में समानांतर भुजाएँ लंबाई में बराबर होती हैं।

Q.3 समलंब चतुर्भुज के कोणों का योग कितना होता है?

Ans. एक चक्रीय समलंब चतुर्भुज के सम्मुख कोणों का योग 180° होता है।

Q.4 समलंब चतुर्भुज का क्षेत्रफल कितना होता है?

Ans. समलंब की “ऊंचाई” दो समानांतर भुजाओं के बीच की लंबवत दूरी है। तब समलम्ब चतुर्भुज का क्षेत्रफल = माध्यिका × ऊँचाई।

Q.5 समांतर चतुर्भुज का सूत्र क्या होता है?

Ans. क्षेत्रफल = आधार × ऊँचाई वह सूत्र है जिसका उपयोग विशेष रूप से समांतर चतुर्भुज के क्षेत्रफल की गणना करने के लिए किया जाता है।

Q.6 समलंब का सूत्र क्या है?

Ans. किसी समलंब चतुर्भुज का क्षेत्रफल इसकी ऊंचाई और इसकी समांतर भुजाओं के गुणनफल के बराबर होता है।

Q.7 क्या सभी वर्ग समलंब चतुर्भुज होते हैं?

Ans. सभी वर्ग, समलंब होते हैं, क्योंकि सभी वर्गों में समानांतर भुजाओं के युग्म होते हैं।

Q.8 समलंब चतुर्भुज कैसे बनता है?

Ans. जिस चतुर्भुज की सम्मुख भुजाओं का केवल एक युग्म समान्तर होता है, समलम्ब चतुर्भुज कहलाता है।

जरूर पढ़िए :

उम्मीद हैं आपको समलंब चतुर्भुज की जानकारी पसंद आयी होगी।

यदि आपको समलंब चतुर्भुज की जानकारी पसंद आयी हो तो दोस्तों के साथ शेयर करें।