Class 4 Maths Solutions Chapter – 6

इस पेज पर हम Class 4 Maths Solutions Chapter – 6 के बारे में सम्पूर्ण जानकारी पढ़ने वाले हैं तो इस आर्टिकल को पूरा जरूर पढ़िए।

पिछले पेज पर हमने गुणा एवं भाग से संबंधित प्रश्नों को हल करना सीखा। एवं पहाड़े को बनाना सीखा।

चलिए इस पेज पर Class 4 Maths Solutions Chapter – 6 के बारे में पड़ेगें।

Class 4 Maths Solutions Chapter – 6

इस पेज पर आप पड़ेगें –

• किसी संख्या के गुणज और गुणनखण्ड निकालना।
• अभाज्य संख्याओं को समझना तथा 100 तक कि अभाज्य संख्याएँ ज्ञात करना।
• किसी संख्या 2, 3, 4, 5, 9, 10, 11 से विभाज्यता के नियम जानना।
• विभाज्यता के नियमों का प्रयोग करना।

गुणज (Multiples)

किसी भी संख्या के गुणज उसके गुणकों के रूप में होगें। अर्थात किसी भी संख्या के गुणनखण्ड या तो उस संख्या के बराबर होंगे या फिर उससे बड़े होंगे।

उदाहरण :

• 5 के गुणज = 5, 10, 15, 20 …………. n
• 10 के गुणज = 10, 20, 30, 40 ….……n

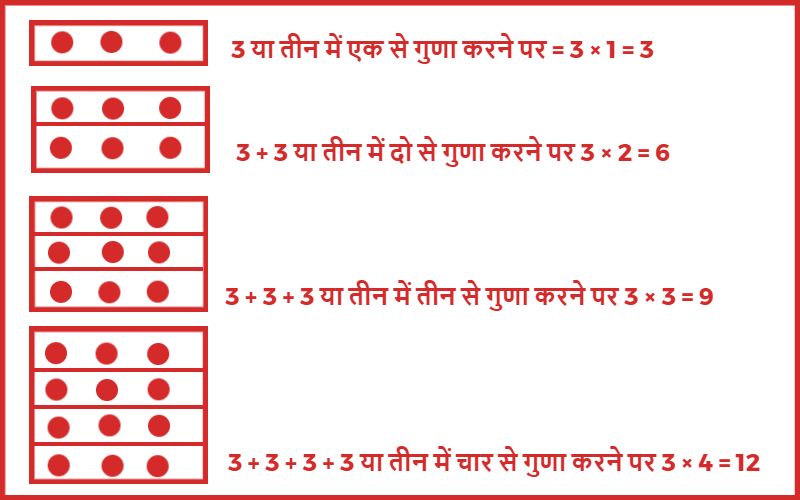
ऊपर दिए उदाहरण में 3 को 1, 2, 3, 4 से गुणा करने पर 3, 6, 9, 12 प्राप्त होता हैं।

3, 6, 9, 12 ………….. संख्या 3 के गुणज कहलाते हैं। गुणज को अपवर्त्य भी कहते हैं।

अभ्यास 6.1

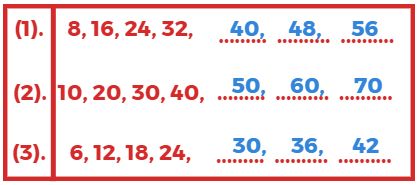
1. निम्नलिखित संख्याओं के अगले तीन गुणज लिखिए?

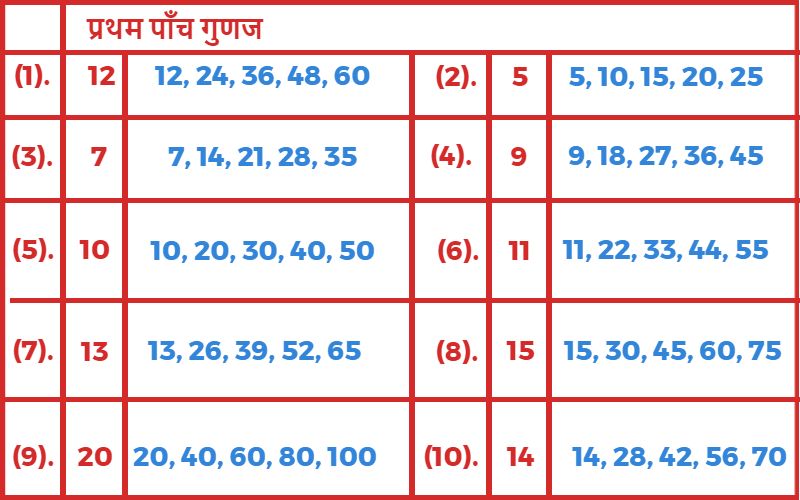
2. निम्नलिखित संख्याओं के प्रथम पाँच गुणज लिखिए?

3. जाँच कीजिए कि क्या :

(1). 3 का गुणज 18 हैं?

3 के गुणज → 3, 6, 9, 12, 15, 18

3 के गुणज में 18 आता हैं इसलिए 3 का गुणज 18 हैं।

(2). 9 का गुणज 27 हैं?

9 के गुणज → 9, 18, 27

9 के गुणज में 27 आता हैं इसलिए 9 का गुणज 27 हैं।

(3). 5 का गुणज 110 हैं?

5 के गुणज → 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110

5 के गुणज में 110 आता हैं इसलिए 5 का गुणज 110 हैं।

(4). 7 का गुणज 57 हैं?

7 के गुणज → 7, 14, 21, 28, 35, 42, 49, 56, 63

7 के गुणज में 57 नहीं आता हैं इसलिए 7 का गुणज 57 नहीं हैं।

(5). 4 का गुणज 37 हैं?

4 के गुणज → 4, 8, 12, 16, 20, 24, 28, 32, 36, 40

4 के गुणज में 37 नहीं आता हैं इसलिए 4 का गुणज 37 नहीं हैं।

4. रिक्त स्थानों की पूर्ति कीजिए?

(1). 5 × 7 = 35 यहाँ 5 तथा 7 का गुणज 35 हैं।
(2). 9 × 6 = 54 यहाँ 9 तथा 6 का गुणज 54 हैं।
(3). 12 × 3 = 36 यहाँ 12 तथा 3 का गुणज 36 हैं।
(4). 6 × 8 × 2 = 96 यहाँ 6, 8 तथा 2 का गुणज 96 हैं।
(5). 10 × 2 × 5 = 100 यहाँ 10, 2 तथा 5 का गुणज 100 हैं।

नीचे दी गयी तालिका को देखिए इसमें 1 से 10 तक की संख्याओं के प्रथम 10 गुणज दिए गए हैं।

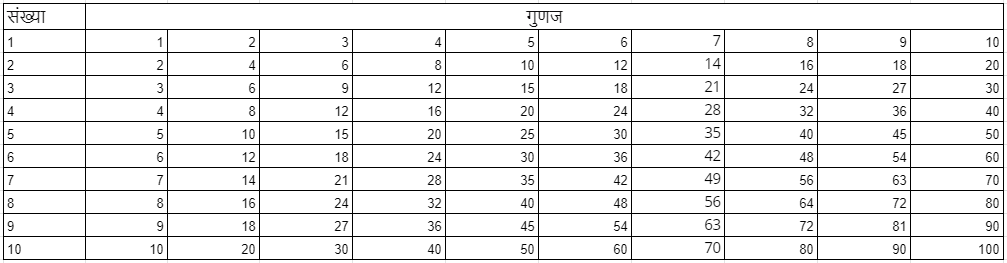
ऊपर दी गई तालिका को देखकर निम्लिखित प्रश्नों के उत्तर दीजिए?

(1). क्या 1 गुणज हैं 3 का?

1 के गुणज → 1, 2, 3

1 के गुणज में 3 आता हैं इसलिए 1 का गुणज 3 हैं।

(2). क्या 1 गुणज हैं 4 का?

1 के गुणज → 1, 2, 3, 4

1 के गुणज में 4 आता हैं इसलिए 1 का गुणज 4 हैं।

(3). क्या 1 गुणज हैं 7 का?

1 के गुणज → 1, 2, 3, 4, 5, 6, 7

1 के गुणज में 7 आता हैं इसलिए 1 का गुणज 7 हैं।

(4). क्या 1 गुणज हैं 10 का?

1 के गुणज → 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

1 के गुणज में 10 आता हैं इसलिए 1 का गुणज 10 हैं।

“प्रत्येक संख्या स्वयं का गुणज होती हैं।“

तालिका देखकर बताइए?

(1). क्या 1 का गुणज 2 हैं?
उत्तर:- हाँ 1 का गुणज 2 हैं?

(2). क्या 1 का गुणज 4 हैं?
उत्तर:- हाँ 1 का गुणज 4 हैं?

(3). क्या 1 का गुणज 7 हैं?
उत्तर:- हाँ 1 का गुणज 7 हैं?

(4). क्या 1 का गुणज 10 हैं?
उत्तर:- हाँ 1 का गुणज 10 हैं?

“प्रत्येक संख्या 1 का गुणज होती हैं।”

गुणनखण्ड (Factor)

दो या अधिक संख्याओं का गुणा करने पर गुणनफल प्राप्त होता हैं। इस प्राप्त गुणनफल में वे सभी संख्याएँ, जिनका गुणा किया जाता हैं, गुणनखण्ड कहलाती हैं।

उदाहरण :

• 5 के गुणनखण्ड = 1 × 3
• 10 के गुणनखण्ड = 2 × 5

भाग के किसी भी प्रश्न में शेषफल शून्य (0) भी हो सकता हैं और नहीं। भी हो सकता हैं।

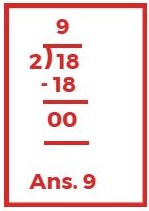
संख्या 2, 18 को पूरी तरह विभाजित करती हैं।
अतः 2 संख्या 18 का गुणनखण्ड हैं।

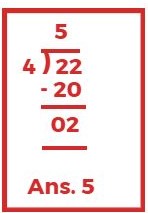
संख्या 4 संख्या 22 को पूरा-पूरा विभाजित नहीं करती हैं।
अतः 4, संख्या 22 का गुणनखण्ड नहीं हैं।

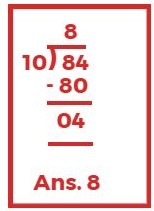
संख्या 10 संख्या 84 को पूरा-पूरा विभाजित नहीं करती हैं।
अतः 10, संख्या 84 का गुणनखण्ड नहीं हैं।

संख्या 15 को 1, 3, 5 तथा 15 से विभाजित कीजिए?

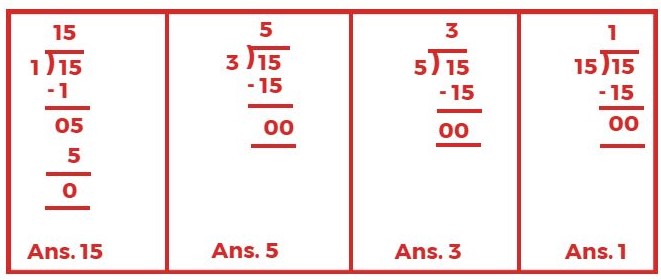
3 तथा 5 दोनों 15 के गुणनखण्ड हैं क्योंकि 3 × 5 = 15

1 तथा 15 भी 15 के गुणनखण्ड हैं क्योंकि 1 × 15 = 15

अतः 1, 3, 5 तथा 15 में से प्रत्येक 15 का गुणनखण्ड हैं।

“जब हम दो संख्याओं का गुणा करते हैं। तो हमें एक गुणनफल प्राप्त होता हैं। उन संख्याओं में से प्रत्येक संख्या गुणनफल का गुणनखण्ड होती हैं।”

गुणनखण्ड से संबंधित महत्वपूर्ण बिन्दु

• 1 प्रत्येक संख्या का गुणनखण्ड होता हैं।
• कोई भी संख्या स्वयं का गुणनखण्ड होती हैं।
• 1 किसी भी संख्या का सबसे छोटा गुणनखण्ड होता हैं।
• किसी संख्या का सबसे बड़ा गुणनखण्ड स्वयं संख्या होती हैं।
• प्रत्येक संख्या (1 को छोड़कर) के कम से कम दो गुणनखण्ड होते हैं। 1 और स्वंम वह संख्या।

अभ्यास 6.2

1. निम्नलिखित प्रश्नों में खाली स्थान भरिए?

(1). 3 × 6 = 18, 3 और 6, गुणनखण्ड हैं 18 के।
(2). 7 × 8 = 56, 7 और 8, गुणनखण्ड हैं 56 के।
(3). 10 × 4 = 40, 10 और 4, गुणनखण्ड हैं 40 के।
(4). 6 × 9 = 54, 6 और 9, गुणनखण्ड हैं 54 के।

2. ज्ञात कीजिए निम्नलिखित में कौन-कौन सी संख्याएँ 18 के गुणनखण्ड हैं।

1, 2, 3, 4, 5, 6, 7, 8, 9, 10

18 के गुणनखण्ड → 2, 3, 3

3. निम्लिखित संख्याओं में प्रत्येक संख्या के दो गुणनखण्ड लिखिए?

(1). 20

20 के गुणनखण्ड → 2, 2

(2). 48

48 के गुणनखण्ड → 2, 2

(3). 72

72 के गुणनखण्ड → 2, 2

(4). 45

45 के गुणनखण्ड → 3, 3

(5). 30

30 के गुणनखण्ड → 2, 3

(6). 100

100 के गुणनखण्ड → 2, 2

4. निम्नलिखित संख्याओं में प्रत्येक के सभी गुणनखण्ड लिखिए?

(1). 9

9 के गुणनखण्ड → 3, 3

(2). 7

7 के गुणनखण्ड → 7

(3). 21

21 के गुणनखण्ड → 3, 7

(4). 25

25 के गुणनखण्ड → 5, 5

(5). 13

13 के गुणनखण्ड → 13

(6). 40

40 के गुणनखण्ड → 2, 2, 2, 5

अभाज्य संख्या

2, 3, 4, 5, 6, 7, 8, ………… में किसी संख्या का भाग देकर देखते हैं कि किस-किस संख्या का पूरा-पूरा भाग जाता हैं।

• संख्या 2 विभाज्य हैं, 1 व 2 से।
• संख्या 3 विभाज्य हैं, 1 व 3 से।
• संख्या 4 विभाज्य हैं, 1, 2 व 4 से।
• संख्या 5 विभाज्य हैं, 1 व 5 से।
• संख्या 6 विभाज्य हैं, 1, 2, 3 व 6 से।

इनमें से संख्या 2, 3, 5 अभाज्य संख्याएँ हैं। क्योंकि ये एक तथा स्वयं के अतिरिक्त किसी अन्य से पूर्णतः विभजित नहीं होती हैं।

1 से 100 तक अभाज्य संख्याओं के लिए सारणी

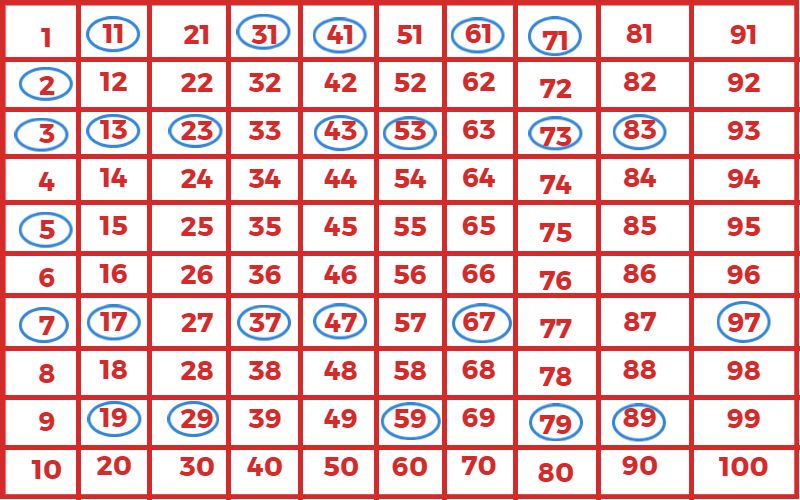
देखिए?

(1). सबसे छोटी अभाज्य संख्या लिखिए जो 8 से बड़ी हो।

उत्तर:- 8 से बड़ी अभाज्य संख्याएँ 11, 13, 17, 19, 23 हैं। इनमें सबसे छोटी संख्या 11 हैं।

(2). सबसे बड़ी अभाज्य संख्या लिखिए जो 18 से छोटी हो।

उत्तर:- 18 से छोटी अभाज्य संख्याएँ 2, 3, 5, 7, 11, 13, 17 हैं। इनमें सबसे बड़ी संख्या 17 हैं।

अभ्यास 6.3

1. सबसे छोटी अभाज्य संख्या लिखिए?

उत्तर:- सबसे छोटी अभाज्य संख्या – 2

2. 17 से बड़ी किंतु सबसे छोटी अभाज्य संख्या लिखिए?

17 से बड़ी किंतु सबसे छोटी अभाज्य संख्या – 19

3. 13 से छोटी परन्तु सबसे बड़ी अभाज्य संख्या लिखिए?

13 से छोटी परन्तु सबसे बड़ी अभाज्य संख्या – 11

4. 20 से छोटी उन अभाज्य संख्याओं के जोड़े लिखिए जिनका अंतर 2 हो?

हल:- प्रश्ननानुसार,
20 से छोटी अभाज्य संख्याएँ – 2, 3, 5, 7, 11, 13, 17, 19
20 से छोटी अभाज्य संख्याओं के बीच 2 का अंतर
(5, 7), (11, 13), (17, 19)

5. ऐसी 50 से छोटी अभाज्य संख्याओं के जोड़े लिखिए जिनका अंतर 1 हो?

50 से छोटी अभाज्य संख्याएँ
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47

50 से छोटी अभाज्य संख्याओं के बीच 1 का अंतर (3 – 2 ) = 1

6. 30 और 40 के बीच की अभाज्य संख्याएँ लिखिए?

30 और 40 के बीच की अभाज्य संख्याएँ – 31, 37 हैं।

7. 50 से छोटी अभाज्य संख्याएँ लिखिए?

50 से छोटी अभाज्य संख्याएँ
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,

8. एक अंक की सभी भाज्य संख्याओं को छाँटिए?

1 अंक की सभी भाज्य संख्या 4, 6, 8 हैं।

विभाज्यता के नियम

2 से विभाज्यता

जिस संख्या में इकाई का अंक 0, 2, 4, 6, व 8 हो, वह संख्या 2 से विभाज्य होती हैं।

जैसे :- संख्या 2228 लेते हैं।

हल :- 2328 का विस्तारित रूप
2328 = (2 × 1000) + (3 × 100) + (2 × 10) + 8
चूंकि संख्या 1000, 100 और 10, 2 से पूर्णतः विभाजित हैं तथा 8 भी 2 से पूर्णतः विभाजित हैं।

2328 भी 2 से पूर्णतः विभाजित होगीं।

जो संख्याएँ 2 से विभाजित हो जाती हैं। उनका इकाई अंक 0, 2, 4, 6, 8 होता हैं।

3 से विभाज्यता

संख्याओं 24, 327, 1215 व 3023 को 3 से भाग कीजिए।
हम देखते हैं कि 24, 327 व 1215 संख्याएँ 3 से विभाजित हो जाती हैं।

संख्या	अंकों का योग
24	2 + 4 = 6
327	3 + 2 + 7 = 12
1215	1 + 2 + 1 + 5 = 9
3023	3 + 0 + 2 + 3 = 8

24, 327, और 1215 के अंकों का योग 3 से पूर्णतः विभाजित हो जाता हैं।

3023 के अंकों का योग 8 हैं जोकि 3 से विभाजित नहीं होता हैं। अतः 3023, 3 से विभाजित नहीं हैं।

यदि किसी संख्या के सभी अंकों का योग 3 से पूरा-पूरा विभाजित हो जाए तो वह संख्या भी 3 से पूरी तरह विभाजित हो जाती हैं।

4 से विभाज्यता

जिस संख्या के दहाई और इकाई के अंकों से बनी संख्या 4 से विभाजित हो जाती हैं वह संख्या भी 4 से पूरी तरह विभाजित हो जाएगी।

जैसे :- संख्या 3456

हल :- 3456 को विस्तार रूप में लिखने पर

3456 = (3 × 1000) + (4 × 100) + 56

इकाई और दहाई के अंकों से बनी संख्या 56 चार से पूर्णतः विभाजित हो जाती हैं। अतः संख्या 3456 भी चार से पूर्णतः विभाजित होती हैं।

5 से विभाज्यता

5 × 1 = 5
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
5 × 5 = 25
5 × 6 = 30
5 × 7 = 35
5 × 8 = 40
5 × 9 = 45
5 × 10 = 50

5, 10, 15, 20, 25, 30, 35, 40, 45, 50 सभी 5 से विभाजित हैं।

किसी भी संख्या का इकाई का अंक शून्य (0) या पाँच (5) हो तो वह 5 से विभाज्य होगी।

9 से विभाज्यता

संख्या	अंकों का योग
18	1 + 8 = 9
36	3 + 6 = 9
171	1 + 7 + 1 = 9
234	2 + 3 + 4 = 9

18, 36, 171, 234 आदि के अंकों का योग 9 आता हैं।

यदि किसी संख्या के अंकों का योग 9 से विभाजित हो जाता हैं तो वह संख्या 9 से विभाजित हो जाएगी।

10 से विभाज्यता

यदि किसी संख्या का इकाई का अंक 0 हो तो वह 10 से विभाज्य होगी।

जैसे :

गुणनखण्ड	इकाई का अंक	10 से विभाज्य हैं या नहीं
100	0	10 से विभाज्य हैं।
117	7	10 से विभाज्य नहीं हैं।

11 से विभाज्यता

यदि किसी संख्या के विषम और सम स्थानों पर आने वाले अंकों के योगफल का अंतर शून्य (0) या 11 से विभाज्य हैं। तो वह संख्या 11 से विभाज्य होगी।

जैसे :

संख्याएँ	सम स्थानों के अंकों का योग	विषम स्थानों के अंकों का योग	अंतर
176	6 + 1 = 7	7	7 – 7 = 0
429	9 + 4 = 13	2	13 – 2 = 11
2365	6 + 2 = 8	5 + 3 = 8	8 – 8 = 0

अतः इनमें से प्रत्येक संख्या 11 से विभाज्य हैं।

अभ्यास 6.4

विभाज्यता के नियमों का प्रयोग करते हुए बताइए?

(1). कौन सी संख्या 2 से विभाजित हैं?

122, 613, 5900, 525, 1210, 730

जिस संख्या में इकाई का अंक 0, 2, 4, 6, व 8 हो, वह संख्या 2 से विभाज्य होती हैं।

(a). 122

हल :- 122 का विस्तारित रूप
122 = (1 × 100) + (2 × 10) + 2
चूंकि संख्या 100 और 10, 2 से पूर्णतः विभाजित हैं तथा 2 भी 2 से पूर्णतः विभाजित हैं।

122 भी 2 से पूर्णतः विभाजित होगीं।

(b). 613

हल :- 2328 का विस्तारित रूप
613 = (6 × 100) + (1 × 10) + 3
चूंकि संख्या 100 और 10, 2 से पूर्णतः विभाजित हैं तथा 3, 2 से विभाजित नहीं हैं।

613, 2 से पूर्णतः विभाजित नहीं हैं।

(c). 5900

हल :- संख्या 5900 में इकाई का अंक 0 हैं।
इसलिए 5900, 2 से पूर्णतः विभाजित हैं।

(d). 525

हल :- 525 का विस्तारित रूप
525 = (5 × 100) + (2 × 10) + 5
चूंकि संख्या 1000, 100 और 10, 2 से पूर्णतः विभाजित हैं तथा 5, 2 से विभाजित नहीं हैं।

525, 2 से पूर्णतः विभाजित नहीं हैं।

(e). 1210

हल :- 1210 का विस्तारित रूप
1210 = (1 × 1000) + (2 × 100) + (1 × 10)
चूंकि संख्या 1000, 100 और 10, 2 से पूर्णतः विभाजित हैं।

अतः 1210 भी 2 से पूर्णतः विभाजित होगीं।

(f). 730

हल :- संख्या 730 में इकाई का अंक 0 हैं।
इसलिए 730, 2 से पूर्णतः विभाजित हैं।

अतः संख्या 122, 5900, 1210, 730 संख्या 2 से पूर्णतः विभाजित होगीं।

(2). कौन सी संख्याएँ 3 से विभाजित हैं?

39, 73, 435, 735, 130, 7821

संख्याओं 39, 73, 435, 735, 130 व 7821 को 3 से भाग कीजिए।

हम देखते हैं कि 39, 435, 735, व 7821 संख्याएँ 3 से विभाजित हो जाती हैं।

संख्या	अंकों का योग
39,	3 + 9 = 12
435	4 + 3 + 5 = 12
735	7 + 3 + 5 = 15
7821	7 + 8 + 2 + 1 = 18

39, 435, 735, व 7821 के अंकों का योग 3 से पूर्णतः विभाजित हो जाता हैं।

73 के अंकों का योग 10 हैं जोकि 3 से विभाजित नहीं होता हैं। और 130 के अंकों का योग 4 हैं जोकि 3 से विभाजित नहीं होता हैं। अतः 73, 130, संख्या 3 से विभाजित नहीं हैं।

यदि किसी संख्या के सभी अंकों का योग 3 से पूरा-पूरा विभाजित हो जाए तो वह संख्या भी 3 से पूरी तरह विभाजित हो जाती हैं।

अतः संख्या 39, 435, 735, व 7821 संख्या 3 से पूर्णतः विभाजित होगीं।

(3). कौन सी संख्याएँ 4 से विभाजित हैं?

81, 318, 5724, 8322, 6422

(a). 5724

हल :- 5724 को विस्तार रूप में लिखने पर

5724 = (5 × 1000) + (7 × 100) + 24

इकाई और दहाई के अंकों से बनी संख्या 24 चार से पूर्णतः विभाजित हो जाती हैं। अतः संख्या 5724 भी चार से पूर्णतः विभाजित होती हैं।

अतः संख्या 5724, 4 से पूर्णतः विभाजित हैं।

(4). कौन सी संख्याएँ 9 से विभाजित हैं?

63, 70, 315, 1341, 117

संख्या	अंकों का योग
63	6 + 3 = 9
315	3 + 1 + 5 = 9
1341	1 + 3 + 4 + 1 = 9
117	1 + 1 + 7 = 9

अतः संख्या 63, 315, 1341, 117 संख्या 9 से पूर्णतः विभाजित होगीं।

(5). कौन सी संख्याएँ 11 से विभाजित हैं?

11, 123, 121, 2365

संख्या	सम स्थानों के अंकों का योग	विषम स्थानों के अंकों का योग	अंतर
11	1 + 1 = 2	1 + 1 = 2	2 – 2 = 0
121	1 + 1 = 2	2	2 -2 = 0
2365	2 + 6 = 8	3 + 5 = 8	8 – 8 = 0

अतः संख्या 11, 121, 2365 संख्या 11 से पूर्णतः विभाजित होगीं।

(6). कौन सी संख्याएँ 5 से विभाजित हैं?

5, 53, 105, 1000, 1285, 1830

किसी भी संख्या का इकाई का अंक शून्य (0) या पाँच (5) हो तो वह 5 से विभाज्य होगी।

5 × 1 = 5
5 × 21 = 105
5 × 200 = 1000
5 × 257 = 1285
5 × 366 = 1830

5, 105, 1000, 1285, 1830 सभी 5 से विभाजित हैं।

अतः संख्या 5, 105, 1000, 1285, 1830 संख्या 5 से पूर्णतः विभाजित होगीं।

जरूर पढ़िए : स्थानीयमान और जातीयमान

उम्मीद हैं आपको की Class 4 Maths Solutions Chapter – 6 जानकारी पसंद आयी होगीं।

यदि आपको Class 4 Maths Solutions Chapter – 6 वाला यह आर्टिकल पसंद आया हो तो सोशल मीडिया पर शेयर कीजिए।