समाकलन की परिभाषा, सूत्र और उदाहरण

इस पेज पर हम समाकलन की समस्त जानकारी को पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए।

पिछले पेज पर हमने पाइथागोरस प्रमेय और थेल्स प्रमेय की जानकारी शेयर की हैं तो उस पोस्ट को भी पढ़े।

चलिए आज हम समाकलन की परिभाषा, सूत्र, प्रकार और उदाहरण की जानकारी को पढ़ते और समझते हैं।

समाकलन किसे कहते हैं

यह एक विशेष प्रकार की योग क्रिया है जिसमें अत्यणु (Infinitesimal) मान वाली किन्तु गिनती में अत्यधिक चर राशियों को जोड़ा जाता है।

इसका एक प्रमुख उपयोग वक्राकार क्षेत्रों का क्षेत्रफल तथा आयतन निकालने में होता है। समाकलन को अवकलन की व्युत्क्रम संक्रिया की तरह भी समझा जा सकता है।

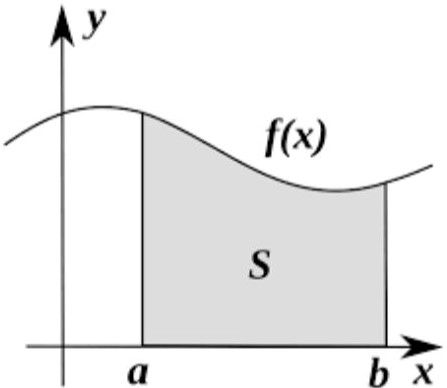
समाकलन के सूत्र

1. ∫x n∙dx = x⁽ⁿ⁺¹⁾/n + 1 + C
2. ∫e^x∙dx = e^x+ C
3. ∫e⁻^x∙dx = -e⁻^x + C
4. ∫1/x∙dx = logₑx + C
5. ∫Sinx∙dx = – Cosx + C
6. ∫Cosx∙dx = Sinx + C
7. ∫Tanx∙dx = log Secx + C
8. ∫Cotx∙dx = log Sinx + C
9. ∫Secx∙dx = log |Secx + Tanx | + C
10. ∫Cosecx∙dx = log |Cosecx – Cotx | + C
11. ∫1/√(1 – x²)∙dx = Sin⁻¹ x + C
12. ∫1/(1 + x²)∙dx = Tan⁻¹ x + C
13. ∫1x(√x² – 1)∙dx = Sec⁻¹ x + C
14. ∫1√(a² – x²)∙dx = Sin⁻¹ (x/a ) + C
15. ∫1√(x² – a²) ∙dx = log | x + √(x² + a²) | + C
16. ∫1√(x² – a²) ∙dx = log | x + √(x² + a²) | + C
17. ∫√(a² – x²) ∙dx = x/2 √(a² – x²) + a²/2 Sin⁻¹( x/a ) + C
18. ∫√(a² + x²)∙dx = x/2 √(a² + x²) + a² /2 log | x + √(x² + a²) | + C
19. ∫√(x² – a²)∙dx = x/2 √(x² – a²) – a²/ 2 log | x + √(x² – a²) | + C
20. ∫1/(a² – x²)∙dx = ½ a log | (a + x)/(a – x)| + C
21. ∫1/( (x² – a²)∙dx = ½ a log | (x – a)/(x + a)| + C
22. ∫Sec²x∙dx = Tanx + C
23. ∫Cosec²x∙dx = -Cotx + C
24. ∫Secx ∙ Tanx∙dx = Secx + C
25. ∫Cosecx ∙ Cotx∙dx = – Cosecx + C
26. ∫K∙dx = Kx + C (जहाँ K = अचर राशि )
27. ∫1/(x² + a²)∙dx = 1/aTan⁻¹ x/a + C

समाकलन के सवाल

प्रश्न 1. निम्न फलनों का x के सापेक्ष समाकलन कीजिए ?

(i). 0
(ii). 1
(iii). x
(iv). x⁹⁹
(v). x⁻¹¹
(vi). x³⁄₂

(i). 0

∫0.dx = 1 [∵ d/dx (1) = 0]

(ii). 1

∫1 dx = x

(iii). x

∫x dx = x¹⁺¹/₁₊₁
½ x²

(iv). x⁹⁹

∫x⁹⁹ dx = x⁹⁹⁺¹/(99+1)
= 1/100 x¹⁰⁰

(v). x⁻¹¹

∫x⁻¹¹ dx = x⁻¹¹⁺¹/(-11+1)
= x⁻¹⁰/-10
= – 1/10 x⁻¹⁰

(vi). x³⁄₂

∫x³⁄₂ dx = x³⁄₂⁺¹/³⁄₂⁺¹
=2/5 x⁵⁄₂

प्रश्न 2. (√x − 1/√x) का x के सापेक्ष समाकलन कीजिए ?

(√x − 1/√x) dx = ∫(x½ − x⁻½) dx
= x½⁻¹/½⁺¹ − x⁻½⁺¹/⁻½⁺¹
= 2x³⁄₂/3 − 2x½

निम्नलिखित फलनों के प्रतिअवकलज (समाकलन) निरीक्षण विधि द्वारा ज्ञात कीजिए।

प्रश्न 1. sin2x

हल:- हम जानते हैं कि 
d/dx cos 2x = – 2 sin 2x
या sin 2x = −1/2 d/dx cos2x
sin 2x = d/dx (−1/2 cos2x)
अतः sin 2x का प्रति अवकलज −1/2 cos 2x है।

प्रश्न 2. cos 3x

हल:- हम जानते हैं कि 
d/dx sin 3x = 3 cos3x
या cos3x = d/dx (1/3 sin 3x)
अत: cos3x का प्रति अवकलज 1/3 sin 3x हैं।

प्रश्न 3. e^2x

हल:- हम जानते हैं कि 
d/dx e^2x = 2e^2x
e^2x = d/dx 1/2 e^2x
अतः e^2x का प्रति अवकलज 1/2 e^2x हैं।

प्रश्न 4. (ax + b)²

हल:- हम जानते हैं कि
d/dx(ax + b)³ = 3a(ax + b)²
(ax + b)² = d/dx[⅓ a(ax + b)³]
अतः (ax + b)² का प्रतिअवकलज 1/3a (ax + b)³ हैं।

प्रश्न 5. sin 2x – 4e^3x

हल:- हम जानते हैं
d/dx cos2x = -2 sin2x
sin 2x = d/dx (-½ cos 2x)
d/dx e³^x = 3e³^x
e³^x = d/dx (1/3 e³^x)
अतः sin 2x – 4e³^x
= d/dx (-½ cos 2x) – 4 d/dx (⅓ e³^x)
d/dx (-½ cos 2x – 4/3 e³^x)

प्रश्न 6. ∫(4e³^x + 1)

हल:- ∫(4e³^x + 1) dx
4∫e³^x dx + ∫1 dx
4 × ⅓ e³^x + x + C
Ans. ⁴⁄₃ e³^x + x + C

प्रश्न 7. ∫x² (1 – 1/x)

हल:- ∫x²(1 – 1/x²) dx
∫x²(x² – 1/x²) dx
∫(x² – 1) dx
∫x² dx – ∫1 dx
Ans. x³⁄₃ – x + C

प्रश्न 8. ∫(ax² + bx + c) dx

हल:- ∫(ax² + bx + c) dx
a∫x² dx + b∫x dx+ c∫1 dx
ax³⁄₃ + bx²⁄₂ + cx + C
Ans. ax³⁄₃ + bx²⁄₂ + cx + C

प्रश्न 9. ∫(2x² + e^x)dx

हल:- ∫(2x² + e^x)dx
2∫x² dx + ∫e^x dx
Ans. 2x³/3 + e^x + C

प्रश्न 10. ∫(√x − 1/√x)² dx

हल:- ∫(√x − 1/√x)² dx
∫(x + 1/x – 2)dx
∫x dx + ∫1/x dx – 2∫1 dx
Ans. x²/2 + log |x – 2x| + C

प्रश्न 11. ∫(x³ + 5x² − 4)/x² dx

हल:- ∫(x³ + 5x² − 4)/x² dx
∫(x³/x² + 5x²/x² − 4/x²) dx
∫x dx + 5∫1 dx – 4∫x⁻² dx
x²/2 + 5x − 4/x + C
Ans. x²/2 + 5x − 4/x + C

प्रश्न 12. ∫(x³ + 3x + 4)/√x dx

हल:- ∫(x³ + 3x + 4)/√x dx
∫(x⁵⁄₂ + 3x³⁄₂ + 4x⁻½) dx
∫x⁵⁄₂ dx + 3 ∫x³⁄₂ dx + 4x⁻½ dx
²⁄₇ x⁷⁄₂ + 3 × ²⁄₃ x⁵⁄₂ + 4 × 2x½ + C
²⁄₇ x⁷⁄₂ + 2 x⁵⁄₂ + 8√x + C
Ans. ²⁄₇ x⁷⁄₂ + 2 x⁵⁄₂ + 8√x + C

प्रश्न 13. ∫(x³ − x² + x − 1)/x − 1 dx

हल:- ∫(x³ − x² + x − 1)/x − 1 dx
अंश के गुणनखण्ड करने पर
∫x² (x − 1) + 1 (x − 1)/x − 1 dx
∫(x² + 1) (x − 1)/x − 1 dx
∫(x² + 1) dx
∫x² dx + ∫1 dx
x³/3 + x + C

प्रश्न 14. ∫(1 − x)√x dx

हल:- ∫(1 − x)√x dx
∫(x½ − x³⁄₂) dx
∫x½ dx − ∫x³⁄₂) dx
⅔ x³⁄₂ − ²⁄₅ x⁵⁄₂ + C
Ans. ⅔ x³⁄₂ − ²⁄₅ x⁵⁄₂ + C

प्रश्न 15. ∫√x (3x² + 2x + 3) dx

हल:- ∫√x (3x² + 2x + 3) dx
∫x½ (3x² + 2x + 3) dx
∫(3x⁵⁄₂ + 2x³⁄₂ + 3x¹⁄₂) dx
3∫x⁵⁄₂ dx + 2∫x³⁄₂ dx + 3∫x¹⁄₂ dx
3 ײ⁄₇ x⁷⁄₂ + 2 × ²⁄₅ x⁵⁄₂ + 3 × ²⁄₃ x³⁄₂
⁶⁄₇ x⁷⁄₂ + ⁴⁄₅ x⁵⁄₂ + 2 x³⁄₂ + C

प्रश्न 16. ∫(2x − 3 cos x + e^x) dx

हल:- ∫(2x − 3 cos x + e^x) dx
2∫x dx − 3 ∫cos x dx + ∫e^x dx
2x²/2 − 3 sin x + e^x + C
Ans. x² − 3 sin x + e^x + C

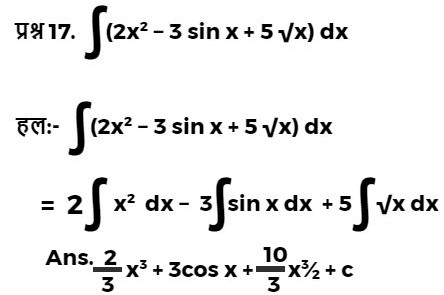
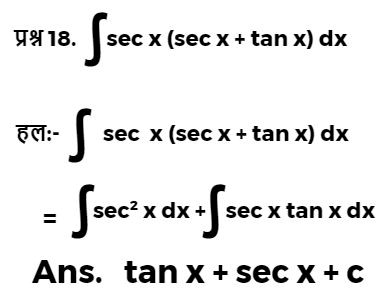
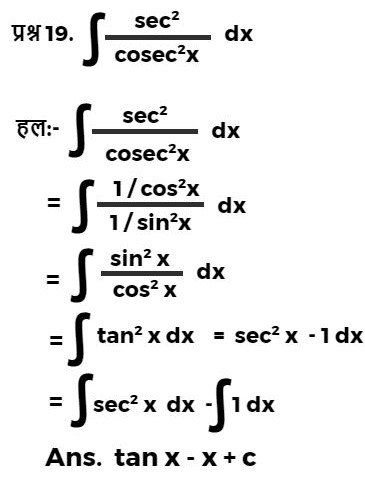
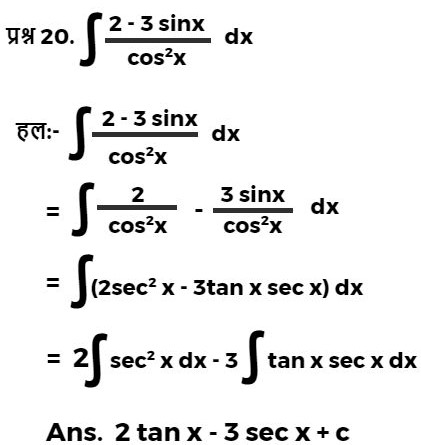
जरूर पढ़िए :
मापन	हीरोन का सूत्र
अवकलन	प्रतिलोम त्रिकोणमितीय फलन

उम्मीद हैं आपको समाकलन की जानकारी पसंद आयी होगी।

यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ शेयर जरूर करें।